We construct two types of unital separable simple 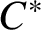 $C^*$-algebras:
$C^*$-algebras: 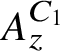 $A_z^{C_1}$ and
$A_z^{C_1}$ and 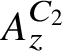 $A_z^{C_2}$, one exact but not amenable, the other nonexact. Both have the same Elliott invariant as the Jiang–Su algebra – namely,
$A_z^{C_2}$, one exact but not amenable, the other nonexact. Both have the same Elliott invariant as the Jiang–Su algebra – namely, 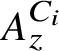 $A_z^{C_i}$ has a unique tracial state,
$A_z^{C_i}$ has a unique tracial state, 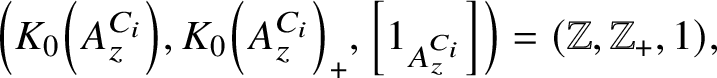 $$ \begin{align*} \left(K_0\left(A_z^{C_i}\right), K_0\left(A_z^{C_i}\right)_+, \left[1_{A_z^{C_i}} \right]\right)=(\mathbb{Z}, \mathbb{Z}_+,1), \end{align*} $$
$$ \begin{align*} \left(K_0\left(A_z^{C_i}\right), K_0\left(A_z^{C_i}\right)_+, \left[1_{A_z^{C_i}} \right]\right)=(\mathbb{Z}, \mathbb{Z}_+,1), \end{align*} $$
and 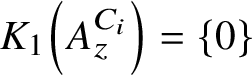 $K_{1}\left (A_z^{C_i}\right )=\{0\}$ (
$K_{1}\left (A_z^{C_i}\right )=\{0\}$ (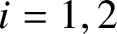 $i=1,2$). We show that
$i=1,2$). We show that 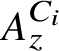 $A_z^{C_i}$ (
$A_z^{C_i}$ (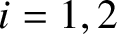 $i=1,2$) is essentially tracially in the class of separable
$i=1,2$) is essentially tracially in the class of separable 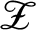 ${\mathscr Z}$-stable
${\mathscr Z}$-stable 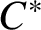 $C^*$-algebras of nuclear dimension
$C^*$-algebras of nuclear dimension 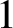 $1$.
$1$. 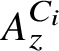 $A_z^{C_i}$ has stable rank one, strict comparison for positive elements and no
$A_z^{C_i}$ has stable rank one, strict comparison for positive elements and no 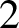 $2$-quasitrace other than the unique tracial state. We also produce models of unital separable simple nonexact (exact but not nuclear)
$2$-quasitrace other than the unique tracial state. We also produce models of unital separable simple nonexact (exact but not nuclear) 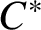 $C^*$-algebras which are essentially tracially in the class of simple separable nuclear
$C^*$-algebras which are essentially tracially in the class of simple separable nuclear 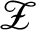 ${\mathscr Z}$-stable
${\mathscr Z}$-stable 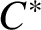 $C^*$-algebras, and the models exhaust all possible weakly unperforated Elliott invariants. We also discuss some basic properties of essential tracial approximation.
$C^*$-algebras, and the models exhaust all possible weakly unperforated Elliott invariants. We also discuss some basic properties of essential tracial approximation.
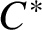 $C^*$-algebras with tracial approximation
$C^*$-algebras with tracial approximation
 ${C}^{\ast }$-algebras
${C}^{\ast }$-algebras