For a non-negative separable random field Z(t), 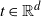$t\in \mathbb{R}^d$, satisfying some mild assumptions, we show that 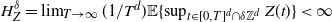$ H_Z^\delta =\lim_{{T} \to \infty} ({1}/{T^d}) \mathbb{E}\{{\sup_{ t\in [0,T]^d \cap \delta \mathbb{Z}^d } Z(t) }\} <\infty$ for 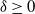$\delta \ge 0$, where 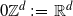$0 \mathbb{Z}^d\,:\!=\,\mathbb{R}^d$, and prove that 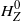$H_Z^0$ can be approximated by 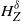$H_Z^\delta$ if 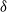$\delta$ tends to 0. These results extend the classical findings for Pickands constants 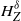$H_{Z}^\delta$, defined for 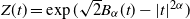$Z(t)= \exp( \sqrt{ 2} B_\alpha (t)- \lvert {t} \rvert^{2\alpha})$, 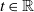$t\in \mathbb{R}$, with 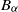$B_\alpha$ a standard fractional Brownian motion with Hurst parameter 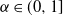$\alpha \in (0,1]$. The continuity of 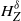$H_{Z}^\delta$ at 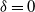$\delta=0$ is additionally shown for two particular extensions of Pickands constants.

The ruin probability in the classical Brownian risk model can be explicitly calculated for both finite and infinite time horizon. This is not the case for the simultaneous ruin probability in the two-dimensional Brownian risk model. Relying on asymptotic theory, we derive in this contribution approximations for both simultaneous ruin probability and simultaneous ruin time for the two-dimensional Brownian risk model when the initial capital increases to infinity.