We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Let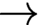 
$\to $ be a continuous 
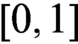$\protect \operatorname {\mathrm {[0,1]}}$-valued function defined on the unit square 
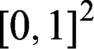$\protect \operatorname {\mathrm {[0,1]}}^2$, having the following properties: (i) 
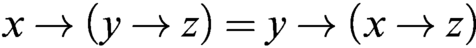$x\to (y\to z)= y\to (x\to z)$ and (ii) 
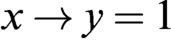$x\to y=1 $ iff 
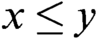$x\leq y$. Let 
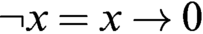$\neg x=x\to 0$. Then the algebra 
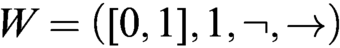$W=(\protect \operatorname {\mathrm {[0,1]}},1,\neg ,\to )$ satisfies the time-honored Łukasiewicz axioms of his infinite-valued calculus. Let 
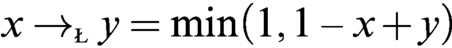$x\to _{\text {\tiny \L }}y=\min (1,1-x+y)$ and 
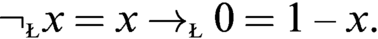$\neg _{\text {\tiny \L }}x=x\to _{\text {\tiny \L }} 0 =1-x.$ Then there is precisely one isomorphism 
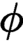$\phi $ of W onto the standard Wajsberg algebra 
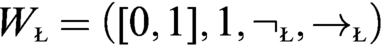$W_{\text {\tiny \L }}= (\protect \operatorname {\mathrm {[0,1]}},1,\neg _{\text {\tiny \L }},\to _{\text {\tiny \L }})$. Thus 
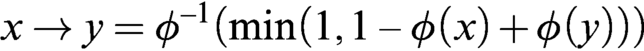$x\to y= \phi ^{-1}(\min (1,1-\phi (x)+\phi (y)))$.
