We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
M. E. Rudin (1971) proved, under CH, that for each P-point p there exists a P-point q strictly RK-greater than p. This result was proved under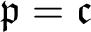 
${\mathfrak {p}= \mathfrak {c}}$ by A. Blass (1973), who also showed that each RK-increasing 
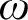$ \omega $-sequence of P-points is upper bounded by a P-point, and that there is an order embedding of the real line into the class of P-points with respect to the RK-ordering. In this paper, the results cited above are proved under the (weaker) assumption that 
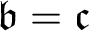$\mathfrak { b}=\mathfrak {c}$. A. Blass asked in 1973 which ordinals can be embedded in the set of P-points, and pointed out that such an ordinal cannot be greater than 
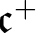$ \mathfrak {c}^{+}$. In this paper it is proved, under 
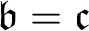$\mathfrak {b}=\mathfrak {c}$, that for each ordinal 
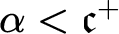$\alpha < \mathfrak {c}^{+}$, there is an order embedding of 
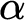$ \alpha $ into P-points. It is also proved, under 
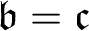$\mathfrak {b}=\mathfrak {c}$, that there is an embedding of the long line into P-points.
