We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We consider the weak closure WZ of the set Z of all feasible pairs (solution, flow) of the family of potential elliptic systems $$ \begin{array}{c}\mbox{div}\left(\sum\limits_{s=1}^{s_0}\sigma_s(x)F_s^\prime (\nabla u(x)+g(x))-f(x)\right)=0\;\mbox{in}\,\Omega, u=(u_1,\dots, u_m)\in H_0^1(\Omega;{\bf R}^m),\;\sigma=(\sigma_1,\dots,\sigma_{s_0})\in S,\end{array} $$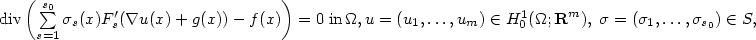 
where Ω ⊂ R n is a bounded Lipschitz domain, F s are strictly convex smooth functions with quadratic growth and $S=\{\sigma\, measurable\,\mid\,\sigma_s(x)=0\;\mbox{or}\,1,\;s=1,\dots,s_0,\;\sigma_1(x)+\cdots +\sigma_{s_0}(x)=1\}$ 
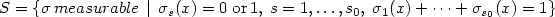. We show that WZ is the zero level set for an integral functional with the integrand $Q\cal F$ 
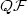being the A-quasiconvex envelope for a certain function $\cal F$ 
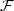and the operator A = (curl,div)m. If the functions F s are isotropic, then on the characteristic cone Λ (defined by the operator A) $Q{\cal F}$ 
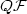coincides with theA-polyconvex envelope of $\cal F$ 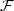and can be computed by means of rank-one laminates.
