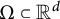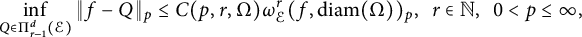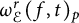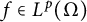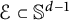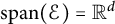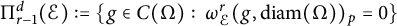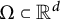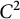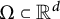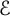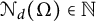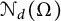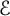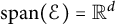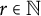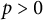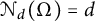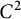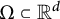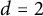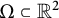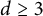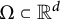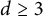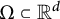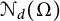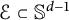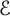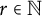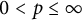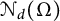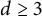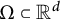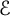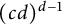This paper studies a new Whitney type inequality on a compact domain 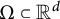$\Omega \subset {\mathbb R}^d$ that takes the form

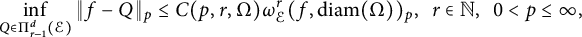
where 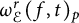$\omega _{\mathcal {E}}^r(f, t)_p$ denotes the rth order directional modulus of smoothness of 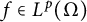$f\in L^p(\Omega )$ along a finite set of directions 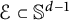$\mathcal {E}\subset \mathbb {S}^{d-1}$ such that 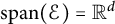$\mathrm {span}(\mathcal {E})={\mathbb R}^d$, 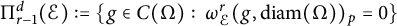$\Pi _{r-1}^d(\mathcal {E}):=\{g\in C(\Omega ):\ \omega ^r_{\mathcal {E}} (g, \mathrm {diam} (\Omega ))_p=0\}$. We prove that there does not exist a universal finite set of directions 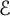$\mathcal {E}$ for which this inequality holds on every convex body 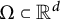$\Omega \subset {\mathbb R}^d$, but for every connected 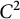$C^2$-domain 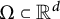$\Omega \subset {\mathbb R}^d$, one can choose 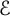$\mathcal {E}$ to be an arbitrary set of d independent directions. 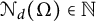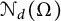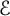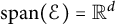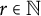We also study the smallest number $\mathcal {N}_d(\Omega )\in {\mathbb N}$ for which there exists a set of $\mathcal {N}_d(\Omega )$ directions $\mathcal {E}$ such that $\mathrm {span}(\mathcal {E})={\mathbb R}^d$ and the directional Whitney inequality holds on $\Omega $ for all $r\in {\mathbb N}$ and 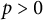$p>0$. It is proved that 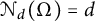$\mathcal {N}_d(\Omega )=d$ for every connected 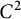$C^2$-domain 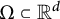$\Omega \subset {\mathbb R}^d$, for 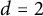$d=2$ and every planar convex body 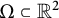$\Omega \subset {\mathbb R}^2$, and for 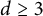$d\ge 3$ and every almost smooth convex body 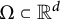$\Omega \subset {\mathbb R}^d$. 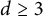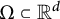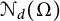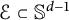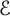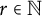For $d\ge 3$ and a more general convex body $\Omega \subset {\mathbb R}^d$, we connect $\mathcal {N}_d(\Omega )$ with a problem in convex geometry on the X-ray number of $\Omega $, proving that if $\Omega $ is X-rayed by a finite set of directions $\mathcal {E}\subset \mathbb {S}^{d-1}$, then $\mathcal {E}$ admits the directional Whitney inequality on $\Omega $ for all $r\in {\mathbb N}$ and 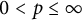$0<p\leq \infty $. Such a connection allows us to deduce certain quantitative estimate of 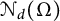$\mathcal {N}_d(\Omega )$ for 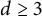$d\ge 3$.

A slight modification of the proof of the usual Whitney inequality in literature also yields a directional Whitney inequality on each convex body 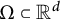$\Omega \subset {\mathbb R}^d$, but with the set 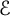$\mathcal {E}$ containing more than 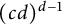$(c d)^{d-1}$ directions. In this paper, we develop a new and simpler method to prove the directional Whitney inequality on more general, possibly nonconvex domains requiring significantly fewer directions in the directional moduli.

We consider a countable number of independent random uniform lines in the hyperbolic plane (in the sense of the theory of geometrical probability) which divide the plane into an infinite number of convex polygonal regions. The main purpose of the paper is to compute the mean number of sides, the mean perimeter, the mean area and the second order moments of these quantities of such polygonal regions. For the Euclidean plane the problem has been considered by several authors, mainly Miles [4]–[9] who has taken it as the starting point of a series of papers which are the basis of the so-called stochastic geometry.