We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We prove by giving an example that when n ≥ 3 the asymptotic behavior of functionals $\int_\Omega \varepsilon|\nabla^2 u|^2+(1-|\nablau|^2)^2/\varepsilon$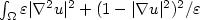 
is quite different with respect to the planar case. In particular weshow that the one-dimensional ansatz due to Aviles and Giga in theplanar case (see [2]) is no longer true in higher dimensions.
