We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
A language L ⊆A*is literally idempotent in case thatua2v ∈ L if and only if uav ∈ L, for each u,v ∈ A*, a ∈ A.Varieties of literally idempotent languages result naturally by takingall literally idempotent languages in a classical (positive) varietyor by considering a certain closure operator on classes of languages.We initiate the systematic study of such varieties. Various classes ofliterally idempotent languages can be characterized using syntactic methods.A starting example is the classof all finite unions of $B^*_1 B^*_2\dots B^*_k$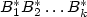 
where B1,...,Bk aresubsets of a given alphabet A.
