In this paper we study the lower semicontinuity problem for a supremalfunctional of the form $F(u,\Omega )= \underset{x\in\Omega}{\rm ess\,sup} f(x,u(x),Du(x))$ 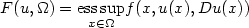 with respect to the strong convergence in L ∞(Ω), furnishing a comparison with the analogous theory developed bySerrin for integrals. A sort of Mazur's lemma for gradients of uniformlyconverging sequences is proved.
with respect to the strong convergence in L ∞(Ω), furnishing a comparison with the analogous theory developed bySerrin for integrals. A sort of Mazur's lemma for gradients of uniformlyconverging sequences is proved.