We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We study the local exactcontrollability problem for the Navier-Stokes equationsthat describe an incompressible fluid flow in a bounded domain Ω with control distributed in a subdomain $\omega\subset\Omega\subset \mathbb{R}^n, n\in\{2,3\}$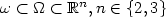 
. The result that we obtained in this paper isas follows. Suppose that $\hat v(t,x)$ 
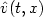is a given solution of theNavier-Stokes equations. Let $ v_0(x)$ 
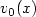be a given initial conditionand $\Vert \hat v(0,\cdot) - v_0 \Vert < \varepsilon$ 
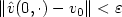where ε is small enough. Then thereexists a locally distributed control $u,\text{supp}\, u\subset (0,T)\times \omega$ 
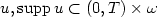such that the solution v(t,x) ofthe Navier-Stokes equations: $$ \partial_tv-\Delta v+(v,\nabla)v=\nabla p+u+f,\,\, \text{\rm div}\, v=0,\,\, v\vert_{\partial\Omega}=0,\,\,v \vert_{t=0} = v_0$$ 
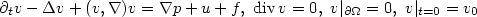coincides with $\hat v(t,x)$ 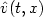at the instant T : $v(T,x) \equiv \hat v(T,x)$ 
.
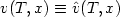