We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We explore the borderline between decidability and undecidability of the following question: “Let C be a class of codes. Given a machine ${\mathfrak{M}}$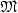 
of type X, is it decidable whether the language $L({{\mathfrak{M}}})$ 
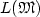lies in C or not?” for codes in general, ω-codes, codes of finite and bounded deciphering delay, prefix, suffix and bi(pre)fix codes, and for finite automata equipped with different versions of push-down stores and counters.
