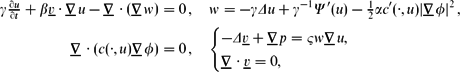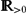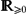We consider a fully practical finite element approximation of the Cahn–Hilliard–Stokes system: 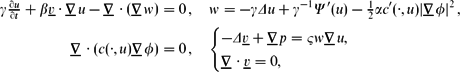 $$\begin{align*}\gamma \tfrac{\partial u}{\partial t} + \beta v \cdot \nabla u -\nabla \cdot \left(\nablaw\right) & = 0 \,, \quadw= -\gamma \Delta u + \gamma ^{-1} \Psi ' (u) - \tfrac12 \alpha c'(\cdot,u)| \nabla \phi |^2\,, \\\nabla \cdot (c(\cdot,u) \nabla \phi) & = 0\,,\quad\begin{cases}-\Delta v + \nabla p = \varsigma w \nabla u,\\\nabla \cdot v = 0, \end{cases}\end{align*}$$
$$\begin{align*}\gamma \tfrac{\partial u}{\partial t} + \beta v \cdot \nabla u -\nabla \cdot \left(\nablaw\right) & = 0 \,, \quadw= -\gamma \Delta u + \gamma ^{-1} \Psi ' (u) - \tfrac12 \alpha c'(\cdot,u)| \nabla \phi |^2\,, \\\nabla \cdot (c(\cdot,u) \nabla \phi) & = 0\,,\quad\begin{cases}-\Delta v + \nabla p = \varsigma w \nabla u,\\\nabla \cdot v = 0, \end{cases}\end{align*}$$ subject to an initial condition u 0(.) ∈ [−1, 1] on the conserved order parameter u ∈ [−1, 1], and mixed boundary conditions. Here, γ ∈ 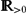 $\mathbb{R}_{>0}$ is the interfacial parameter, α ∈
$\mathbb{R}_{>0}$ is the interfacial parameter, α ∈ 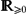 $\mathbb{R}_{\geq0}$ is the field strength parameter, Ψ is the obstacle potential, c(⋅, u) is the diffusion coefficient, and c′(⋅, u) denotes differentiation with respect to the second argument. Furthermore, w is the chemical potential, φ is the electro-static potential, and (v , p) are the velocity and pressure. The system has been proposed to model the manipulation of morphologies in organic solar cells with the help of an applied electric field and kinetics.
$\mathbb{R}_{\geq0}$ is the field strength parameter, Ψ is the obstacle potential, c(⋅, u) is the diffusion coefficient, and c′(⋅, u) denotes differentiation with respect to the second argument. Furthermore, w is the chemical potential, φ is the electro-static potential, and (v , p) are the velocity and pressure. The system has been proposed to model the manipulation of morphologies in organic solar cells with the help of an applied electric field and kinetics.