Our results in this paper increase the model-theoretic precision of a widely usedmethod for building ultrafilters, and so advance the general problem ofconstructing ultrafilters whose ultrapowers have a precise degree of saturation.We begin by showing that any flexible regular ultrafilter makes the product ofan unbounded sequence of finite cardinals large, thus saturating any stabletheory. We then prove directly that a “bottleneck” in theinductive construction of a regular ultrafilter on λ(i.e., a point after which all antichains of ${\cal P}\left( \lambda \right)/{\cal D}$ have cardinality less than λ)essentially prevents any subsequent ultrafilter from being flexible, thus fromsaturating any nonlow theory. The constructions are as follows. First, weconstruct a regular filter ${\cal D}$ on λ so that any ultrafilterextending ${\cal D}$ fails to ${\lambda ^ + }$-saturate ultrapowers of the random graph, thus of any unstabletheory. The proof constructs the omitted random graph type directly. Second,assuming existence of a measurable cardinal κ, weconstruct a regular ultrafilter on $\lambda > \kappa$ which is λ-flexible but not ${\kappa ^{ + + }}$-good, improving our previous answer to a question raised inDow (1985). Third, assuming a weakly compact cardinalκ, we construct an ultrafilter to show that ${\rm{lcf}}\left( {{\aleph _0}} \right)$ may be small while all symmetric cuts of cofinalityκ are realized. Thus certain families of precutsmay be realized while still failing to saturate any unstable theory.

Criteria are obtained for a filter 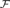${\cal F}$ of subsets of a set I to be an intersectionof finitely many ultrafilters, respectively, finitely manyκ-complete ultrafilters for a given uncountablecardinal $\kappa .$ From these, general results are deduced concerninghomomorphisms on infinite direct product groups, which yield quick proofs ofsome results in the literature: the Łoś–Edatheorem (characterizing homomorphisms from a not-necessarily-countable directproduct of modules to a slender module), and some results of Nahlus and theauthor on homomorphisms on infinite direct products ofnot-necessarily-associative k-algebras. The same tools allowother results of Nahlus and the author to be nontrivially strengthened, andyield an analog to one of their results, with nonabelian groups taking the placeof k-algebras.

We briefly examine the question of how the common technique used in applying thegeneral results of this note to k-algebras on the one hand, andto nonabelian groups on the other, might be extended to more general varietiesof algebras in the sense of universal algebra.

In a final section, the Erdős–Kaplansky theorem ondimensions of vector spaces 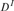${D^I}$ $(D$ a division ring) is extended to reduced products ${D^I}/{\cal F},$ and an application is noted.