We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Let N, X 1, X 2, · ·· be non-constant independent random variables with X 1, X 2, · ·· being identically distributed and N being non-negative and integer-valued. It is shown that the independence of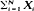 
and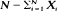 
implies that the Xi 's have a Bernoulli distribution and N has a Poisson distribution. Other related characterization results are considered.
