Refine search
Actions for selected content:
9 results
Ageing and stochastic comparisons for a covariate failure model
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 39 / Issue 2 / June 2002
- Published online by Cambridge University Press:
- 14 July 2016, pp. 421-425
- Print publication:
- June 2002
-
- Article
- Export citation
Signatures of indirect majority systems
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 38 / Issue 2 / June 2001
- Published online by Cambridge University Press:
- 14 July 2016, pp. 597-603
- Print publication:
- June 2001
-
- Article
- Export citation
A general shock model for a reliability system
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 37 / Issue 4 / December 2000
- Published online by Cambridge University Press:
- 14 July 2016, pp. 925-935
- Print publication:
- December 2000
-
- Article
- Export citation
General Conditions for Comparing the Reliability Functions of Systems of Components Sharing a Common Environment
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 35 / Issue 1 / March 1998
- Published online by Cambridge University Press:
- 14 July 2016, pp. 124-135
- Print publication:
- March 1998
-
- Article
- Export citation
Reliability analysis for systems in a random environment
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 34 / Issue 4 / December 1997
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1021-1031
- Print publication:
- December 1997
-
- Article
- Export citation
Comparison of system reliability functions under laboratory and common operating environments
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 34 / Issue 2 / June 1997
- Published online by Cambridge University Press:
- 14 July 2016, pp. 536-545
- Print publication:
- June 1997
-
- Article
- Export citation
Reliability of a consecutive-k-out-of-n system in a random environment
-
- Journal:
- Journal of Applied Probability / Volume 27 / Issue 2 / June 1990
- Published online by Cambridge University Press:
- 14 July 2016, pp. 452-458
- Print publication:
- June 1990
-
- Article
- Export citation
Multivariate distributions for the life lengths of components of a system sharing a common environment
-
- Journal:
- Journal of Applied Probability / Volume 23 / Issue 2 / June 1986
- Published online by Cambridge University Press:
- 14 July 2016, pp. 418-431
- Print publication:
- June 1986
-
- Article
- Export citation
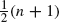 , and use this to show that the expected lifetime of an
, and use this to show that the expected lifetime of an 