We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Let S be a set of n points in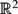 
${\mathbb R}^{2}$ contained in an algebraic curve C of degree d. We prove that the number of distinct distances determined by S is at least cdn 4/3, unless C contains a line or a circle.
We also prove the lower bound cd ′ min{m 2/3 n 2/3, m 2, n 2} for the number of distinct distances between m points on one irreducible plane algebraic curve and n points on another, unless the two curves are parallel lines, orthogonal lines, or concentric circles. This generalizes a result on distances between lines of Sharir, Sheffer and Solymosi in [19].
