In this paper, we study asymmetric Ramsey properties of the random graph 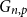$G_{n,p}$. Let 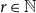$r \in \mathbb{N}$ and 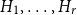$H_1, \ldots, H_r$ be graphs. We write 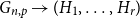$G_{n,p} \to (H_1, \ldots, H_r)$ to denote the property that whenever we colour the edges of 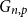$G_{n,p}$ with colours from the set 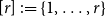$[r] \,{:\!=}\, \{1, \ldots, r\}$ there exists 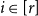$i \in [r]$ and a copy of 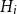$H_i$ in 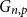$G_{n,p}$ monochromatic in colour 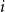$i$. There has been much interest in determining the asymptotic threshold function for this property. In several papers, Rödl and Ruciński determined a threshold function for the general symmetric case; that is, when 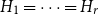$H_1 = \cdots = H_r$. A conjecture of Kohayakawa and Kreuter from 1997, if true, would fully resolve the asymmetric problem. Recently, the 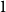$1$-statement of this conjecture was confirmed by Mousset, Nenadov and Samotij.

Building on work of Marciniszyn, Skokan, Spöhel and Steger from 2009, we reduce the 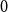$0$-statement of Kohayakawa and Kreuter’s conjecture to a certain deterministic subproblem. To demonstrate the potential of this approach, we show this subproblem can be resolved for almost all pairs of regular graphs. This therefore resolves the 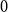$0$-statement for all such pairs of graphs.