We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
In this paper, we construct the first examples of complex surfaces of general type with arbitrarily large geometric genus whose canonical maps induce non-hyperelliptic fibrations of genus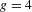 
$g=4$, and on the other hand, we prove that there is no complex surface of general type whose canonical map induces a hyperelliptic fibrations of genus 
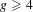$g\geqslant 4$ if the geometric genus is large.
