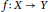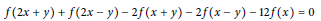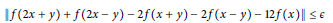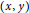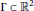Refine search
Actions for selected content:
1 results
Cubic Functional Equations on Restricted Domains of Lebesgue Measure Zero
-
- Journal:
- Canadian Mathematical Bulletin / Volume 60 / Issue 1 / 01 March 2017
- Published online by Cambridge University Press:
- 20 November 2018, pp. 95-103
- Print publication:
- 01 March 2017
-
- Article
-
- You have access
- Export citation
-
Let
$X$ be a real normed space, 
$Y$ a Banach space, and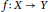 
$f\,:\,X\,\to \,Y$ . We prove theUlam–Hyers stability theorem for the cubic functional equation
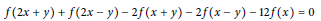$$f\left( 2x\,+\,y \right)\,+\,f\left( 2x\,-\,y \right)\,-\,2f\left( x\,+\,y \right)\,-\,2f\left( x\,-\,y \right)\,-\,12f\left( x \right)\,=\,0$$in restricted domains. As an application we consider a measure zero stability problem of the inequality
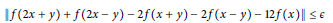$$\left\| f\left( 2x\,+\,y \right)\,+\,f\left( 2x\,-\,y \right)\,-\,2f\left( x\,+\,y \right)\,-\,2f\left( x\,-\,y \right)\,-\,12f\left( x \right) \right\|\,\le \,\varepsilon$$for all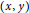
$\left( x,\,y \right)$ in 
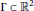$\Gamma \,\subset \,{{\mathbb{R}}^{2}}$ of Lebesgue measure 0.
