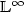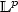Refine search
Actions for selected content:
6 results
Nash equilibrium payoffs for stochastic differential games withreflection
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 19 / Issue 4 / October 2013
- Published online by Cambridge University Press:
- 27 August 2013, pp. 1189-1208
- Print publication:
- October 2013
-
- Article
- Export citation
A game interpretation of the Neumann problem for fullynonlinear parabolic and elliptic equations
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 19 / Issue 4 / October 2013
- Published online by Cambridge University Press:
- 13 August 2013, pp. 1109-1165
- Print publication:
- October 2013
-
- Article
- Export citation
Dynamic programming principle for stochastic recursive optimalcontrol problem with delayed systems∗
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 18 / Issue 4 / October 2012
- Published online by Cambridge University Press:
- 16 January 2012, pp. 1005-1026
- Print publication:
- October 2012
-
- Article
- Export citation
Linearization techniques for $\mathbb{L}^{\infty}$
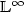 See PDF-control problemsand dynamic programming principles in classical and $\mathbb{L}^{\infty}$
See PDF-control problemsand dynamic programming principles in classical and $\mathbb{L}^{\infty}$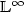 See PDF-control problems
See PDF-control problems
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 18 / Issue 3 / July 2012
- Published online by Cambridge University Press:
- 17 August 2011, pp. 836-855
- Print publication:
- July 2012
-
- Article
- Export citation
Dynamic Programming Principle for tug-of-war games withnoise
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 18 / Issue 1 / January 2012
- Published online by Cambridge University Press:
- 02 December 2010, pp. 81-90
- Print publication:
- January 2012
-
- Article
- Export citation
Unbounded viscosity solutions of hybrid control systems
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 16 / Issue 1 / January 2010
- Published online by Cambridge University Press:
- 19 December 2008, pp. 176-193
- Print publication:
- January 2010
-
- Article
- Export citation