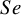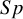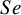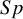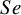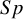A meta-analysis of diagnostic test accuracy (DTA) studies typically synthesizes study-specific test sensitivity (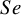$Se$) and specificity (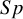$Sp$) to quantify the accuracy of an index test of interest. The bivariate linear mixed effects model with logit transformation of 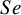$Se$ and 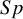$Sp$ (BLMM-Logit) is commonly used to make statistical inferences, but may lead to misleading results due to the need for Haldane–Anscombe correction and an approximate estimation of variance within the study. Alternative models based on the arcsine square root and Freeman–Tukey double arcsine transformation have been proposed to address these issues; however, they still rely on approximate variance estimation, which is suitable only for large sample sizes. The bivariate generalized linear mixed effects model (BGLMM) is another option, but it faces convergence issues with small meta-analyses or sparse primary studies. To address these limitations, we proposed an exact within-study variance calculation method that does not require Haldane–Anscombe correction and is applicable regardless of the transformation used or the number of studies and participants. We evaluated this method against existing approaches using real-life and simulated DTA meta-analyses. The methods were comparable for large meta-analyses. However, BLMM-Logit demonstrated substantial negative bias in estimating variances between studies and consistently underestimated summary 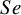$Se$ and 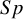$Sp$ in all simulation scenarios. In contrast, the proposed exact methods (Exact-Logit, Exact-ASR, and Exact-FTDA) and BGLMM had minimal bias and better performance metrics, particularly for meta-analyses with sparse primary studies. Thus, the proposed exact methods should be preferred for DTA meta-analyses with small or sparse studies.