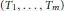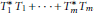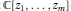Refine search
Actions for selected content:
1 results
Irreducible Tuples Without the Boundary Property
-
- Journal:
- Canadian Mathematical Bulletin / Volume 58 / Issue 1 / 01 March 2015
- Published online by Cambridge University Press:
- 20 November 2018, pp. 9-18
- Print publication:
- 01 March 2015
-
- Article
-
- You have access
- Export citation
-
We examine spectral behavior of irreducible tuples that do not admit the boundary property.In particular, we prove under some mild assumption that the spectral radius of such an
$m$ -tuple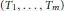 
$\left( {{T}_{1}},\,.\,.\,.\,,\,{{T}_{m}} \right)$ must be the operator norm of 
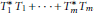$T_{1}^{*}\,{{T}_{1}}\,+\,.\,.\,.\,+\,T_{m}^{*}{{T}_{m}}$ . We use this simple observation to ensure the boundary property for an irreducible, essentially normal, joint q-isometry, provided it is not a joint isometry. We further exhibit a family of reproducing Hilbert 
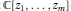$\mathbb{C}\left[ {{z}_{1}},\,.\,.\,.\,,{{z}_{m}} \right]$ -modules (of which the Drury–Arveson Hilbert module is a prototype) with the property that any two nested unitarily equivalent submodules are indeed equal.
