The complexity of computing, via threshold circuits, the iteratedproduct and powering of fixed-dimension $k\times k$ 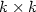 matriceswith integer or rational entries is studied. We call these twoproblems $\sf IMP_k$
matriceswith integer or rational entries is studied. We call these twoproblems $\sf IMP_k$ 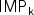 and $\sf MPOW_k$
and $\sf MPOW_k$ 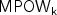 , respectively, for short. We prove that: (i) For $k\geq2$
, respectively, for short. We prove that: (i) For $k\geq2$ 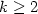 , $\sf IMP_k$
, $\sf IMP_k$ 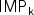 does not belong to ${\rm TC}^0$
does not belong to ${\rm TC}^0$ 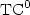 , unless ${\rm TC}^0={\rm NC}^1$
, unless ${\rm TC}^0={\rm NC}^1$ 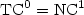 .newline(ii) For stochastic matrices : $\sf IMP_2$
.newline(ii) For stochastic matrices : $\sf IMP_2$ 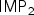 belongs to ${\rm TC}^0$
belongs to ${\rm TC}^0$ 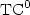 while, for $k\geq3$
while, for $k\geq3$ 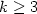 , $\sf IMP_k$
, $\sf IMP_k$ 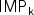 does not belong to ${\rm TC}^0$
does not belong to ${\rm TC}^0$ 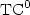 , unless ${\rm TC}^0={\rm NC}^1$
, unless ${\rm TC}^0={\rm NC}^1$ 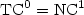 . (iii) For any k, $\sf MPOW_k$
. (iii) For any k, $\sf MPOW_k$ 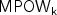 belongs to ${\rm TC}^0$
belongs to ${\rm TC}^0$ 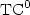 .
.