We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Let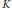 
$K$ be a knot in 
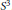${{S}^{3}}$ . This paper is devoted to Dehn surgeries which create 3-manifolds containing a closed non-orientable surface 
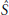$\hat{S}$ . We look at the slope 
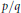$p/q$ of the surgery, the Euler characteristic 
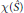$\mathcal{X}(\hat{S})$ of the surface and the intersection number 
$s$ between 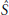$\hat{S}$ and the core of the Dehn surgery. We prove that if 
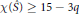$\mathcal{X}(\hat{S})\,\ge \,15\,-3q$ , then 
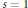$s\,=\,1$ . Furthermore, if 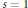$s\,=\,1$ then 
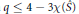$q\,\le \,4\,-\,3\,\mathcal{X}(\hat{S})$ or 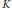$K$ is cabled and 
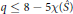$q\,\le \,8\,-5\mathcal{X}(\hat{S})$ . As consequence, if 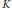$K$ is hyperbolic and 
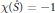$\mathcal{X}(\hat{S})\,=\,-1$ , then 
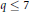$q\,\le \,7$ .
