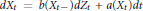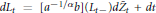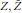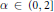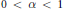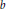Refine search
Actions for selected content:
1 results
The Time Change Method and SDEs with Nonnegative Drift
-
- Journal:
- Canadian Mathematical Bulletin / Volume 53 / Issue 3 / 01 September 2010
- Published online by Cambridge University Press:
- 20 November 2018, pp. 503-515
- Print publication:
- 01 September 2010
-
- Article
-
- You have access
- Export citation
-
Using the time change method we show how to construct a solution to the stochastic equation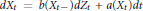
$d{{X}_{t}}\,=\,b({{X}_{t}}\_)d{{Z}_{t}}\,+\,a({{X}_{t}})dt$ with a nonnegative drift a provided there exists a solution to the auxililary equation 
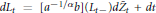$d{{L}_{t}}=[{{a}^{-1/\alpha }}b]({{L}_{t}}\_)d\overline{{{Z}_{t}}}+dt$ where 
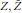$Z,\,\overline{Z}$ are two symmetric stable processes of the same index 
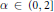$\alpha \,\in \,(0,\,2]$ . This approach allows us to prove the existence of solutions for both stochastic equations for the values 
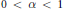$0\,<\,\alpha \,<\,1$ and only measurable coefficients 
$a$ and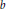 
$b$ satisfying some conditions of boundedness. The existence proof for the auxililary equation uses the method of integral estimates in the sense of Krylov.
