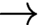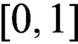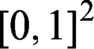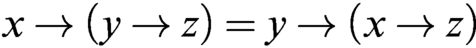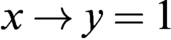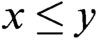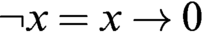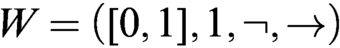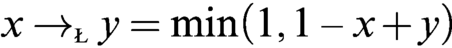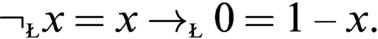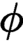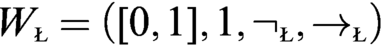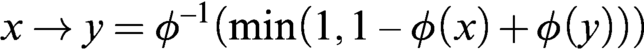Refine search
Actions for selected content:
1 results
WHAT THE ŁUKASIEWICZ AXIOMS MEAN
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 30 October 2020, pp. 906-917
- Print publication:
- September 2020
-
- Article
- Export citation
-
Let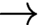
$\to $ be a continuous 
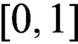$\protect \operatorname {\mathrm {[0,1]}}$-valued function defined on the unit square 
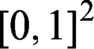$\protect \operatorname {\mathrm {[0,1]}}^2$, having the following properties: (i) 
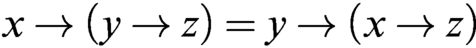$x\to (y\to z)= y\to (x\to z)$ and (ii) 
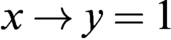$x\to y=1 $ iff 
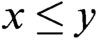$x\leq y$. Let 
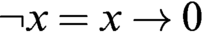$\neg x=x\to 0$. Then the algebra 
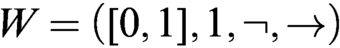$W=(\protect \operatorname {\mathrm {[0,1]}},1,\neg ,\to )$ satisfies the time-honored Łukasiewicz axioms of his infinite-valued calculus. Let 
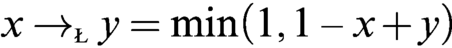$x\to _{\text {\tiny \L }}y=\min (1,1-x+y)$ and 
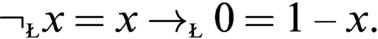$\neg _{\text {\tiny \L }}x=x\to _{\text {\tiny \L }} 0 =1-x.$ Then there is precisely one isomorphism 
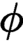$\phi $ of W onto the standard Wajsberg algebra 
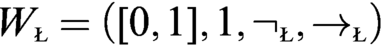$W_{\text {\tiny \L }}= (\protect \operatorname {\mathrm {[0,1]}},1,\neg _{\text {\tiny \L }},\to _{\text {\tiny \L }})$. Thus 
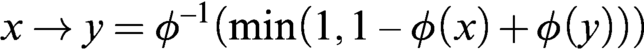$x\to y= \phi ^{-1}(\min (1,1-\phi (x)+\phi (y)))$.
