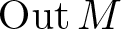Refine search
Actions for selected content:
1 results
Every locally compact group is the outer automorphism group of a II1 factor
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 28 March 2025, pp. 1-12
-
- Article
- Export citation
-
We prove that every locally compact second countable group G arises as the outer automorphism group
$\operatorname{Out} M$ of a II1 factor, which was so far only known for totally disconnected groups, compact groups, and a few isolated examples. We obtain this result by proving that every locally compact second countable group is a centralizer group, a class of Polish groups that arise naturally in ergodic theory and that may all be realized as 
$\operatorname{Out} M$.
