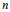The invariantlyharmonic functions in the unit ball${\Bbb B}^n$in ${\Bbb C}^n$ are those annihilated by theBergman Laplacian $\Delta$. The Poisson-Szeg\"o kernel $P(z,\zeta)$ solves the Dirichlet problem for$\Delta$: if $f\in C(S^n)$, the Poisson-Szeg\"o transform of $f$, $P[f](z)=\int_{S^n}P(z,\zeta)f(\zeta)\,d\sigma(\zeta),$ where $d\sigma$ is the normalized Lebesgue measure on $S^n$, is the uniqueinvariantly harmonic function $u$ in ${\Bbb B}^n$, continuous up to the boundary, such that $u=f$ on$S^n$. The Poisson-Szeg\"o transform establishes, loosely speaking, a one-to-one correspondencebetween function theory in $S^n$ and invariantly harmonic function theory in ${\Bbb B}^n$.When$n\geq 2$, it is natural to consider on $S^n$ function spaces related to its natural non-isotropicmetric, for these are the spaces arising from complex analysis. In the paper, differentcharacterizations of such spaces of smooth functions are given in terms of their invariantly harmonicextensions, using maximal functions and area integrals, as in the corresponding Euclidean theory.Particular attention is given to characterization in terms of purely radial or purely tangentialderivatives. The smoothness is measured in two different scales: that of Sobolev spaces and that ofLipschitz spaces, including BMO and Besov spaces.

1991 Mathematics Subject Classification:32A35, 32A37, 32M15, 42B25.

A class of Toeplitz type operators acting on the weighted Bergman spaces of the unit ball in the $n$ -dimensional complex space is considered and two pluriharmonic symbols of commuting Toeplitz type operators are completely characterized.