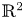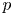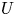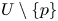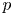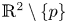Refine search
Actions for selected content:
1 results
Global centres in a class of quintic polynomial differential systems
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 11 April 2024, pp. 1-16
-
- Article
- Export citation
-
A centre of a differential system in the plane $ {\mathbb {R}}^2$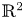
is an equilibrium point $p$
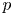having a neighbourhood $U$
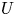such that $U\setminus \{p\}$
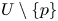is filled with periodic orbits. A centre $p$
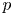is global when $ {\mathbb {R}}^2\setminus \{p\}$
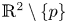is filled with periodic orbits. In general, it is a difficult problem to distinguish the centres from the foci for a given class of differential systems, and also it is difficult to distinguish the global centres inside the centres. The goal of this paper is to classify the centres and the global centres of the following class of quintic polynomial differential systems\begin{align*} \dot{x}= y,\quad \dot{y}={-}x+a_{05}\,y^5+a_{14}\,x\,y^4+a_{23}\,x^2\,y^3+a_{32}\,x^3\,y^2+a_{41}\,x^4\,y+a_{50}\,x^5, \end{align*}in the plane $ {\mathbb {R}}^2$
.
