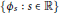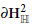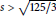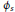Refine search
Actions for selected content:
1 results
A Note on Quaternionic Hyperbolic Ideal Triangle Groups
-
- Journal:
- Canadian Mathematical Bulletin / Volume 59 / Issue 2 / 01 June 2016
- Published online by Cambridge University Press:
- 20 November 2018, pp. 244-257
- Print publication:
- 01 June 2016
-
- Article
-
- You have access
- Export citation
-
In this paper, the quaternionic hyperbolic ideal triangle groups are parametrized by a real one-parameter family
$\{{{\phi }_{s}}\,:\,s\,\in \,\mathbb{R}\}$ . The indexing parameter s is the tangent of the quaternionic angular invariant of a triple of points in 
$\partial \mathbf{H}_{\mathbb{H}}^{2}$ forming this ideal triangle. We show that if 
$s>\sqrt{125/3},$ then 
${{\phi }_{S}}$ is not a discrete embedding, and if 
$s\,\le \,\sqrt{3\text{5}}$ , then ${{\phi }_{S}}$ is a discrete embedding.
