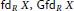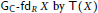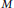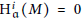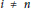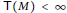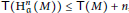Refine search
Actions for selected content:
1 results
On Flat and Gorenstein Flat Dimensions of Local Cohomology Modules
-
- Journal:
- Canadian Mathematical Bulletin / Volume 59 / Issue 2 / 01 June 2016
- Published online by Cambridge University Press:
- 20 November 2018, pp. 403-416
- Print publication:
- 01 June 2016
-
- Article
-
- You have access
- Export citation
-
Let
$\mathfrak{a}$ be an ideal of a Noetherian local ring 
$R$ and let 
$C$ be a semidualizing $R$ -module. For an $R$ -module 
$X$ , we denote any of the quantities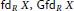 
$\text{f}{{\text{d}}_{R}}X,\,\text{Gf}{{\text{d}}_{R}}X$ and 
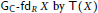${{\text{G}}_{\text{C}}}-\text{f}{{\text{d}}_{R}}\,X\,\text{by}\,\text{T}\left( X \right)$ . Let 
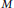$M$ be an $R$ -module such that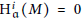 
$\text{H}_{\mathfrak{a}}^{i}\left( M \right)\,=\,0$ for all 
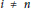$i\,\ne \,n$ . It is proved that if 
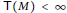$T\left( M \right)\,<\,\infty$ , then 
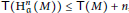$\text{T}\left( \text{H}_{\mathfrak{a}}^{n}\left( M \right) \right)\,\le \,\text{T}\left( M \right)\,+\,n$ , and the equality holds whenever 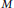$M$ is finitely generated. With the aid of these results, among other things, we characterize Cohen–Macaulay modules, dualizing modules, and Gorenstein rings.
