We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
The problem of synchronizing a networkof identical processors that work synchronouslyat discrete steps is studied. Processors are arranged as an array ofm rows and n columns and can exchange each other only one bitof information.We give algorithms whichsynchronize square arrays of (n × n) processors and give somegeneral constructions to synchronize arrays of (m × n) processors.Algorithms are given to synchronize in time n 2, $n \lceil \log n\rceil$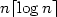 
, $n\lceil\sqrt n \rceil$ 
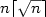and 2n a square array of (n × n) processors.Our approach is a modular description ofsynchronizing algorithms in terms of "fragments" of cellular automata that are calledsignals.Compositional rules to obtain new signals (and new synchronizationtimes) starting from known ones are given for an (m × n) array.Using these compositional rules we constructsynchronizations in any "feasible" linear time and in any time expressedby a polynomial with nonnegative coefficients.
