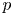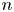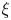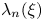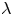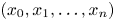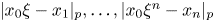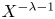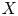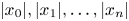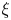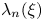Refine search
Actions for selected content:
1 results
On simultaneous rational approximation to a p-adic number and its integral powers, II
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 2 / May 2021
- Published online by Cambridge University Press:
- 07 May 2021, pp. 317-337
-
- Article
- Export citation
-
Let $p$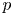
be a prime number. For a positive integer $n$
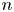and a real number $\xi$
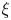, let $\lambda _n (\xi )$
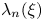denote the supremum of the real numbers $\lambda$
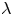for which there are infinitely many integer tuples $(x_0, x_1, \ldots , x_n)$
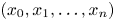such that $| x_0 \xi - x_1|_p, \ldots , | x_0 \xi ^{n} - x_n|_p$
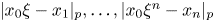are all less than $X^{-\lambda - 1}$
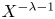, where $X$
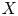is the maximum of $|x_0|, |x_1|, \ldots , |x_n|$
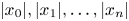. We establish new results on the Hausdorff dimension of the set of real numbers $\xi$
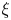for which $\lambda _n (\xi )$
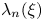is equal to (or greater than or equal to) a given value.
