We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
In this paper, we consider a Borel measurable function on the space of $\scriptstyle m\times n$ 
matrices $\scriptstyle f: M^{m\times n}\rightarrow \bar{\mathbb{R}}$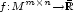 
taking the value $ \scriptstyle +\infty$ 
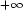, such that its rank-one-convex envelope $\scriptstyle Rf$ 
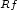is finite and satisfies for some fixed $\scriptstyle p>1$ 
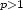: $$\scriptstyle -c_0\leq Rf(F)\leq c(1+\Vert F\Vert^p)\ \hbox{for all}\F\in M^{m\times n},$$ 
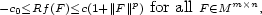where $\scriptstyle c,c_0>0$ 
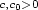. Let $\scriptstyle\O$ 
be a given regular bounded open domain of $\scriptstyle \mathbb{R}^n$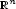 
. We define on $\scriptstyle W^{1,p}(\O;\mathbb{R}^m)$ 
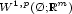the functional $$\scriptstyle I(u)=\int_{\O}f(\nabla u(x))\ dx.$$ 
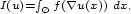Then, under some technical restrictions on $\scriptstyle f$ 
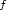, we show that the relaxed functional $\scriptstyle\bar I$ 
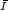for the weak topology of $\scriptstyle W^{1,p}(\O;\mathbb{R}^m)$ 
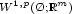has the integral representation: $$\scriptstyle \bar I(u)=\int_{\O}Q[Rf](\nabla u(x))\ dx,$$ 
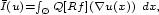where for a given function $\scriptstyle g$ 
, $\scriptstyle Qg$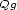 
denotes its quasiconvex envelope.
