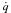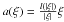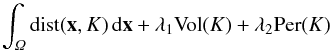Refine search
Actions for selected content:
6997 results in Mathematical modeling and methods
Maximum principle for optimal control of fully coupledforward-backward stochastic differential delayed equations∗
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 18 / Issue 4 / October 2012
- Published online by Cambridge University Press:
- 16 January 2012, pp. 1073-1096
- Print publication:
- October 2012
-
- Article
- Export citation
The structure of reachable sets for affine control systemsinduced by generalized Martinet sub-Lorentzian metrics
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 18 / Issue 4 / October 2012
- Published online by Cambridge University Press:
- 16 January 2012, pp. 1150-1177
- Print publication:
- October 2012
-
- Article
- Export citation
A variational problem for couples of functions andmultifunctions with interaction between leaves
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 18 / Issue 4 / October 2012
- Published online by Cambridge University Press:
- 16 January 2012, pp. 1178-1206
- Print publication:
- October 2012
-
- Article
- Export citation
Variational analysis for a nonlinear elliptic problem on theSierpiński gasket
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 18 / Issue 4 / October 2012
- Published online by Cambridge University Press:
- 16 January 2012, pp. 941-953
- Print publication:
- October 2012
-
- Article
- Export citation
Dynamic programming principle for stochastic recursive optimalcontrol problem with delayed systems∗
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 18 / Issue 4 / October 2012
- Published online by Cambridge University Press:
- 16 January 2012, pp. 1005-1026
- Print publication:
- October 2012
-
- Article
- Export citation
Continuity of solutions of a nonlinear ellipticequation
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 19 / Issue 1 / January 2013
- Published online by Cambridge University Press:
- 16 January 2012, pp. 1-19
- Print publication:
- January 2013
-
- Article
- Export citation
Adaptive finite element method for shape optimization∗
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 18 / Issue 4 / October 2012
- Published online by Cambridge University Press:
- 16 January 2012, pp. 1122-1149
- Print publication:
- October 2012
-
- Article
- Export citation
On convex sets that minimize the averagedistance
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 18 / Issue 4 / October 2012
- Published online by Cambridge University Press:
- 16 January 2012, pp. 1049-1072
- Print publication:
- October 2012
-
- Article
- Export citation
Nash equilibria for a model of traffic flow with several groupsof drivers
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 18 / Issue 4 / October 2012
- Published online by Cambridge University Press:
- 16 January 2012, pp. 969-986
- Print publication:
- October 2012
-
- Article
- Export citation
Linear-quadratic optimal control for the Oseen equations withstabilized finite elements
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 18 / Issue 4 / October 2012
- Published online by Cambridge University Press:
- 16 January 2012, pp. 987-1004
- Print publication:
- October 2012
-
- Article
- Export citation
Asymptotic stability of stationary solutions to thedrift-diffusion model in the whole space
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 18 / Issue 4 / October 2012
- Published online by Cambridge University Press:
- 16 January 2012, pp. 1097-1121
- Print publication:
- October 2012
-
- Article
- Export citation
Multiplicity of solutions for the noncooperativep-Laplacian operator elliptic system with nonlinear boundaryconditions
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 18 / Issue 4 / October 2012
- Published online by Cambridge University Press:
- 16 January 2012, pp. 930-940
- Print publication:
- October 2012
-
- Article
- Export citation
Continuous dependence estimates for the ergodic problem ofBellman-Isaacs operators via the parabolic Cauchy problem∗
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 18 / Issue 4 / October 2012
- Published online by Cambridge University Press:
- 16 January 2012, pp. 954-968
- Print publication:
- October 2012
-
- Article
- Export citation
Initial-boundary value problems for second order systems ofpartial differential equations∗
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 46 / Issue 3 / May 2012
- Published online by Cambridge University Press:
- 11 January 2012, pp. 559-593
- Print publication:
- May 2012
-
- Article
- Export citation
Preface - Special volume in honor of Professor David Gottlieb
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 46 / Issue 3 / May 2012
- Published online by Cambridge University Press:
- 11 January 2012, p. 513
- Print publication:
- May 2012
-
- Article
-
- You have access
- Export citation
A priori convergence of the Greedy algorithmfor the parametrized reduced basis method
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 46 / Issue 3 / May 2012
- Published online by Cambridge University Press:
- 11 January 2012, pp. 595-603
- Print publication:
- May 2012
-
- Article
- Export citation
Iterative schemes for high order compact discretizations to the exterior Helmholtz equation∗
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 46 / Issue 3 / May 2012
- Published online by Cambridge University Press:
- 11 January 2012, pp. 647-660
- Print publication:
- May 2012
-
- Article
- Export citation
Numerical approximation of the inviscid 3D primitive equations in a limited domain
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 46 / Issue 3 / May 2012
- Published online by Cambridge University Press:
- 11 January 2012, pp. 619-646
- Print publication:
- May 2012
-
- Article
- Export citation
P-adaptive Hermite methods for initial value problems∗
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 46 / Issue 3 / May 2012
- Published online by Cambridge University Press:
- 11 January 2012, pp. 545-557
- Print publication:
- May 2012
-
- Article
- Export citation
Coarse quantization for random interleaved sampling ofbandlimited signals∗∗∗
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 46 / Issue 3 / May 2012
- Published online by Cambridge University Press:
- 11 January 2012, pp. 605-618
- Print publication:
- May 2012
-
- Article
- Export citation