We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
The first and last papers of Harald Bohr deal with ordinary Dirichlet series 
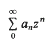
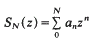
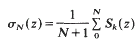
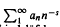and their order (or Lindelöf) function μ(σ) (= inf{α;f(σ + it) + 0(|t|α)}). The Lindelöf hypothesis is μ(σ) = inf(0, ½ − t) when an = (−1)n. Are there ordinary Dirichlet series with −l < μ′ (σ) < 0 for some σ? A negative answer would imply Lindelöf's hypothesis. This is the last problem of Harald Bohr. This paper gives (1) a review on Bohr's results on ordinary Dinchlet series; (2) a review on results of the author and of Queffelec on “almost sure” and “quasi sure” properties of series 
with the solution of a previous problem of Bohr; (3) the following answer to the last problem: μ′(σ) can approach − ½, and necessarily μ(σ + μ(σ) + ½) = 0. The characterization of the order functions of ordinary Dirichlet series remains an open question.
