Refine listing
Actions for selected content:
65 results in 20Jxx
The cohomology ring of a combinatorially aspherical group
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 47 / Issue 3 / December 1989
- Published online by Cambridge University Press:
- 09 April 2009, pp. 453-457
- Print publication:
- December 1989
-
- Article
-
- You have access
- Export citation
The kernel of integral cup product
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 43 / Issue 1 / August 1987
- Published online by Cambridge University Press:
- 09 April 2009, pp. 10-15
- Print publication:
- August 1987
-
- Article
-
- You have access
- Export citation
Epimorphisms preserving perfect radicals
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 36 / Issue 3 / June 1984
- Published online by Cambridge University Press:
- 09 April 2009, pp. 357-364
- Print publication:
- June 1984
-
- Article
-
- You have access
- Export citation
Some applications of group Obstructions
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 32 / Issue 2 / April 1982
- Published online by Cambridge University Press:
- 09 April 2009, pp. 178-186
- Print publication:
- April 1982
-
- Article
-
- You have access
- Export citation
A model for the classifying space of an extra special p-group
- Part of
-
- Journal:
- Mathematika / Volume 22 / Issue 2 / December 1975
- Published online by Cambridge University Press:
- 26 February 2010, pp. 182-187
- Print publication:
- December 1975
-
- Article
- Export citation
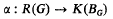
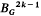 denotes the (2k − l)-skeleton of
denotes the (2k − l)-skeleton of