Refine listing
Actions for selected content:
23 results in 94Bxx
A POLYNOMIAL RING CONSTRUCTION FOR THE CLASSIFICATION OF DATA
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 79 / Issue 2 / April 2009
- Published online by Cambridge University Press:
- 13 March 2009, pp. 213-225
- Print publication:
- April 2009
-
- Article
-
- You have access
- Export citation
Counting irreducible Goppa codes
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 71 / Issue 3 / December 2001
- Published online by Cambridge University Press:
- 09 April 2009, pp. 299-306
- Print publication:
- December 2001
-
- Article
-
- You have access
- Export citation
Double circulant constructions of the Leech lattice
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 69 / Issue 3 / December 2000
- Published online by Cambridge University Press:
- 09 April 2009, pp. 287-297
- Print publication:
- December 2000
-
- Article
-
- You have access
- Export citation
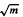 in the Leech lattice. We give such a construction by means of double circulant codes whenever
in the Leech lattice. We give such a construction by means of double circulant codes whenever 