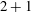Refine listing
Actions for selected content:
25 results in 65Pxx
A BIOLOGICAL TREATMENT OF INDUSTRIAL WASTEWATERS: CONTOIS KINETICS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 56 / Issue 4 / April 2015
- Published online by Cambridge University Press:
- 30 April 2015, pp. 397-415
-
- Article
-
- You have access
- Export citation
PLANE WAVE STABILITY OF THE SPLIT-STEP FOURIER METHOD FOR THE NONLINEAR SCHRÖDINGER EQUATION
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 2 / 01 July 2014
- Published online by Cambridge University Press:
- 10 April 2014, e5
-
- Article
-
- You have access
- Open access
- Export citation
BLOW-UP OF THE NONEQUIVARIANT (
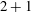 $2+1$)-DIMENSIONAL WAVE MAP
$2+1$)-DIMENSIONAL WAVE MAP
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 55 / Issue 2 / October 2013
- Published online by Cambridge University Press:
- 18 March 2014, pp. 151-161
-
- Article
-
- You have access
- Export citation
ON THE EXISTENCE OF CHAOTIC BEHAVIOUR IN PURE AND SIMPLE MICROBIAL COMPETITION: THE ROLE OF CONTOIS KINETICS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 55 / Issue 2 / October 2013
- Published online by Cambridge University Press:
- 21 November 2013, pp. 162-174
-
- Article
-
- You have access
- Export citation
RECONSIDERING TRIGONOMETRIC INTEGRATORS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 50 / Issue 3 / January 2009
- Published online by Cambridge University Press:
- 03 November 2009, pp. 320-332
-
- Article
-
- You have access
- Export citation