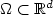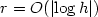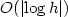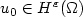Refine search
Actions for selected content:
4288 results in Numerical analysis and computational science
Compressible two-phase flows by centraland upwind schemes
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 38 / Issue 3 / May 2004
- Published online by Cambridge University Press:
- 15 June 2004, pp. 477-493
- Print publication:
- May 2004
-
- Article
- Export citation
A new two-dimensional Shallow Water model including pressure effects and slow varying bottom topography
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 38 / Issue 2 / March 2004
- Published online by Cambridge University Press:
- 15 March 2004, pp. 211-234
- Print publication:
- March 2004
-
- Article
- Export citation
Stick-slip transition capturing by usingan adaptive finite element method
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 38 / Issue 2 / March 2004
- Published online by Cambridge University Press:
- 15 March 2004, pp. 249-260
- Print publication:
- March 2004
-
- Article
- Export citation
Convergence of a high-order compact finite difference scheme for a nonlinear Black–Scholes equation
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 38 / Issue 2 / March 2004
- Published online by Cambridge University Press:
- 15 March 2004, pp. 359-369
- Print publication:
- March 2004
-
- Article
- Export citation
A note on (2K+1)-point conservative monotone schemes
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 38 / Issue 2 / March 2004
- Published online by Cambridge University Press:
- 15 March 2004, pp. 345-357
- Print publication:
- March 2004
-
- Article
- Export citation
Galerkin time-stepping methods for nonlinear parabolic equations
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 38 / Issue 2 / March 2004
- Published online by Cambridge University Press:
- 15 March 2004, pp. 261-289
- Print publication:
- March 2004
-
- Article
- Export citation
Energetics and switching of quasi-uniform statesin small ferromagnetic particles
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 38 / Issue 2 / March 2004
- Published online by Cambridge University Press:
- 15 March 2004, pp. 235-248
- Print publication:
- March 2004
-
- Article
- Export citation
A Maxwell-Bloch model with discrete symmetries for wave propagation in nonlinear crystals: an application to KDP
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 38 / Issue 2 / March 2004
- Published online by Cambridge University Press:
- 15 March 2004, pp. 321-344
- Print publication:
- March 2004
-
- Article
- Export citation
Analysis of gradient flow of a regularized Mumford-Shahfunctional for image segmentation and image inpainting
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 38 / Issue 2 / March 2004
- Published online by Cambridge University Press:
- 15 March 2004, pp. 291-320
- Print publication:
- March 2004
-
- Article
- Export citation
Error estimates in the fast multipole methodfor scattering problemsPart 1: Truncation of the Jacobi-Anger series
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 38 / Issue 2 / March 2004
- Published online by Cambridge University Press:
- 15 March 2004, pp. 371-394
- Print publication:
- March 2004
-
- Article
- Export citation
Mixed formulations for a class of variational inequalities
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 38 / Issue 1 / January 2004
- Published online by Cambridge University Press:
- 15 February 2004, pp. 177-201
- Print publication:
- January 2004
-
- Article
- Export citation
A posteriori error control for the Allen–Cahn problem: circumventing Gronwall's inequality
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 38 / Issue 1 / January 2004
- Published online by Cambridge University Press:
- 15 February 2004, pp. 129-142
- Print publication:
- January 2004
-
- Article
- Export citation
Nouvelles formulations intégrales pour les problèmesde diffraction d'ondes
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 38 / Issue 1 / January 2004
- Published online by Cambridge University Press:
- 15 February 2004, pp. 157-175
- Print publication:
- January 2004
-
- Article
- Export citation
Fast deterministic pricing of optionson Lévy driven assets
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 38 / Issue 1 / January 2004
- Published online by Cambridge University Press:
- 15 February 2004, pp. 37-71
- Print publication:
- January 2004
-
- Article
- Export citation
Dynamical behavior of Volterra model with mutual interferenceconcerning IPM
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 38 / Issue 1 / January 2004
- Published online by Cambridge University Press:
- 15 February 2004, pp. 143-155
- Print publication:
- January 2004
-
- Article
- Export citation
A quasi-dual Lagrange multiplier space for serendipity mortar finite elements in 3D
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 38 / Issue 1 / January 2004
- Published online by Cambridge University Press:
- 15 February 2004, pp. 73-92
- Print publication:
- January 2004
-
- Article
- Export citation
The effect of reduced integrationin the Steklov eigenvalue problem
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 38 / Issue 1 / January 2004
- Published online by Cambridge University Press:
- 15 February 2004, pp. 27-36
- Print publication:
- January 2004
-
- Article
- Export citation
Numerical solution of parabolic equationsin high dimensions
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 38 / Issue 1 / January 2004
- Published online by Cambridge University Press:
- 15 February 2004, pp. 93-127
- Print publication:
- January 2004
-
- Article
- Export citation
The existence of a solution and a numerical method for the Timoshenko nonlinear wave system
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 38 / Issue 1 / January 2004
- Published online by Cambridge University Press:
- 15 February 2004, pp. 1-26
- Print publication:
- January 2004
-
- Article
- Export citation
A posteriori ErrorEstimates For the 3D Stabilized Mortar Finite Element Methodapplied to the Laplace Equation
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 37 / Issue 6 / November 2003
- Published online by Cambridge University Press:
- 15 November 2003, pp. 991-1011
- Print publication:
- November 2003
-
- Article
- Export citation