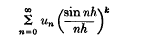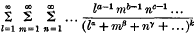Refine search
Actions for selected content:
26204 results in Theoretical Physics and Mathematical Physics
Concerning some Solutions of the Boundary Layer Equations in Hydrodynamics
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 26 / Issue 1 / January 1930
- Published online by Cambridge University Press:
- 24 October 2008, pp. 1-30
- Print publication:
- January 1930
-
- Article
- Export citation
Note on the Theory of Measure
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 26 / Issue 1 / January 1930
- Published online by Cambridge University Press:
- 24 October 2008, pp. 88-93
- Print publication:
- January 1930
-
- Article
- Export citation
A property of continuous arcs
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 26 / Issue 1 / January 1930
- Published online by Cambridge University Press:
- 24 October 2008, pp. 31-33
- Print publication:
- January 1930
-
- Article
- Export citation
Note on Eddy Current Losses in the Sheaths of Rectifier Cables
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 26 / Issue 1 / January 1930
- Published online by Cambridge University Press:
- 24 October 2008, pp. 115-116
- Print publication:
- January 1930
-
- Article
- Export citation
A Geometrical Study of the Hyper-Octohedral Group
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 26 / Issue 1 / January 1930
- Published online by Cambridge University Press:
- 24 October 2008, pp. 94-98
- Print publication:
- January 1930
-
- Article
- Export citation
The relation between Riemann's method of summation and Cesàro's
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 26 / Issue 1 / January 1930
- Published online by Cambridge University Press:
- 24 October 2008, pp. 34-42
- Print publication:
- January 1930
-
- Article
- Export citation
Proceedings at the Meetings held during the Session 1928–1929
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 25 / Issue 4 / October 1929
- Published online by Cambridge University Press:
- 24 October 2008, pp. 530-540
- Print publication:
- October 1929
-
- Article
- Export citation
Some formulae for surfaces in higher space
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 25 / Issue 4 / October 1929
- Published online by Cambridge University Press:
- 24 October 2008, pp. 390-406
- Print publication:
- October 1929
-
- Article
- Export citation
An Analysis of Triode Valve Rectification. Part II
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 25 / Issue 4 / October 1929
- Published online by Cambridge University Press:
- 24 October 2008, pp. 482-490
- Print publication:
- October 1929
-
- Article
- Export citation
On the emission of electrons from metals covered by thin films, in intense electric fields
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 25 / Issue 4 / October 1929
- Published online by Cambridge University Press:
- 24 October 2008, pp. 454-460
- Print publication:
- October 1929
-
- Article
- Export citation
The Fields Close to a Radiating Aerial
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 25 / Issue 4 / October 1929
- Published online by Cambridge University Press:
- 24 October 2008, pp. 491-507
- Print publication:
- October 1929
-
- Article
- Export citation
On the Convergence of a certain Multiple Series
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 25 / Issue 4 / October 1929
- Published online by Cambridge University Press:
- 24 October 2008, pp. 410-411
- Print publication:
- October 1929
-
- Article
- Export citation
Note concerning the β particles of very small Energy emitted during Radioactive Transformation
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 25 / Issue 4 / October 1929
- Published online by Cambridge University Press:
- 24 October 2008, pp. 522-529
- Print publication:
- October 1929
-
- Article
- Export citation
A Note on the Stability of a Valve Amplifier
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 25 / Issue 4 / October 1929
- Published online by Cambridge University Press:
- 24 October 2008, pp. 508-513
- Print publication:
- October 1929
-
- Article
- Export citation
Statement of Accounts of the Cambridge Philosophical Society, from January 1, 1928, to December 31, 1928
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 25 / Issue 4 / October 1929
- Published online by Cambridge University Press:
- 24 October 2008, pp. 541-542
- Print publication:
- October 1929
-
- Article
- Export citation
The Production of High Speed Electrons by Indirect Means
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 25 / Issue 4 / October 1929
- Published online by Cambridge University Press:
- 24 October 2008, pp. 469-481
- Print publication:
- October 1929
-
- Article
- Export citation
PSP volume 25 issue 4 Cover and Front matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 25 / Issue 4 / October 1929
- Published online by Cambridge University Press:
- 24 October 2008, p. f1
- Print publication:
- October 1929
-
- Article
-
- You have access
- Export citation
On the Hesse-Cayley Algorithm for a Plane Quartic whose Bitangents are all Real
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 25 / Issue 4 / October 1929
- Published online by Cambridge University Press:
- 24 October 2008, pp. 433-435
- Print publication:
- October 1929
-
- Article
- Export citation
A deduction of the formula for the product of two incidence symbols in the case of lines and planes
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 25 / Issue 4 / October 1929
- Published online by Cambridge University Press:
- 24 October 2008, pp. 384-389
- Print publication:
- October 1929
-
- Article
- Export citation
Current Distribution near edges of Discharge-Tube Cathodes
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 25 / Issue 4 / October 1929
- Published online by Cambridge University Press:
- 24 October 2008, pp. 461-468
- Print publication:
- October 1929
-
- Article
- Export citation
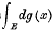 is not continuous there exists a countable set ε
is not continuous there exists a countable set ε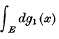 such that
such that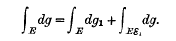
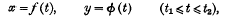
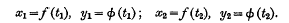
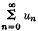 is said to be summable by Riemann's method of order
is said to be summable by Riemann's method of order