Hostname: page-component-5d84bcc8dc-8ls8l Total loading time: 0 Render date: 2026-09-12T23:42:02.258Z Has data issue: false hasContentIssue false
  • English
  • Français

$\alpha$-Stable convergence of heavy-/light-tailed infinitely wide neural networks

Part of: Inference from stochastic processes Limit theorems Stochastic processes

Published online by Cambridge University Press:  03 July 2023

Paul Jung ,
Hoil Lee Open the ORCID record for Hoil Lee [Opens in a new window] ,
Jiho Lee  and
Hongseok Yang
Paul Jung*
Affiliation:
Sam Houston State University
Hoil Lee*
Affiliation:
KAIST
Jiho Lee*
Affiliation:
Korea Science Academy of KAIST
Hongseok Yang*
Affiliation:
KAIST and Institute for Basic Science
*
*Postal address: Department of Mathematics and Statistics, 1905 University Ave, Huntsville, TX 77340, USA. Email address: phj001@shsu.edu
***Postal address: Department of Mathematics and Computer Sciences, Korea Science Academy of KAIST, 105-47, Baegyanggwanmun-ro, Busanjin-gu, Busan 47162, Republic of Korea. Email address: efidiaf@gmail.com
***Postal address: Department of Mathematics and Computer Sciences, Korea Science Academy of KAIST, 105-47, Baegyanggwanmun-ro, Busanjin-gu, Busan 47162, Republic of Korea. Email address: efidiaf@gmail.com
****Postal address: School of Computing and Kim Jaechul Graduate School of AI, KAIST, 291 Daehak-ro, Yuseong-gu, Daejeon 34141, Republic of Korea; Discrete Mathematics Group, Institute for Basic Science, 55 Expo-ro, Yuseong-gu, Daejeon 34126, Republic of Korea. Email address: hongseok.yang@kaist.ac.kr
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider infinitely wide multi-layer perceptrons (MLPs) which are limits of standard deep feed-forward neural networks. We assume that, for each layer, the weights of an MLP are initialized with independent and identically distributed (i.i.d.) samples from either a light-tailed (finite-variance) or a heavy-tailed distribution in the domain of attraction of a symmetric $\alpha$-stable distribution, where 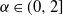$\alpha\in(0,2]$ may depend on the layer. For the bias terms of the layer, we assume i.i.d. initializations with a symmetric $\alpha$-stable distribution having the same $\alpha$ parameter as that layer. Non-stable heavy-tailed weight distributions are important since they have been empirically seen to emerge in trained deep neural nets such as the ResNet and VGG series, and proven to naturally arise via stochastic gradient descent. The introduction of heavy-tailed weights broadens the class of priors in Bayesian neural networks. In this work we extend a recent result of Favaro, Fortini, and Peluchetti (2020) to show that the vector of pre-activation values at all nodes of a given hidden layer converges in the limit, under a suitable scaling, to a vector of i.i.d. random variables with symmetric $\alpha$-stable distributions, 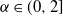$\alpha\in(0,2]$.

Keywords

Heavy-tailed distributionstable processmulti-layer perceptronsinfinite-width limitweak convergence

MSC classification

Primary: 60F05: Central limit and other weak theorems
Secondary: 60G52: Stable processes 62M45: Neural nets and related approaches

Information

Type
Original Article
Information
Advances in Applied Probability , Volume 55 , Issue 4 , December 2023 , pp. 1415 - 1441
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of Applied Probability Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Aldous, D. J. (1986). Classical convergence of triangular arrays, stable laws and Schauder’s fixed-point theorem. Adv. Appl. Prob. 18, 9–14.Google Scholar
Arora, S. (2019). On exact computation with an infinitely wide neural net. In Advances in Neural Information Processing Systems 32 (NeurIPS 2019), Neural Information Processing Systems Foundation, San Diego, CA, pp. 8141–8150.Google Scholar
Durrett, R. (2019). Probability: Theory and Examples. Cambridge University Press.CrossRefGoogle Scholar
Favaro, S., Fortini, S. and Peluchetti, S. (2020). Stable behaviour of infinitely wide deep neural networks. Preprint. Available at https://arxiv.org/abs/2003.00394.Google Scholar
Favaro, S., Fortini, S. and Peluchetti, S. (2021). Deep stable neural networks: large-width asymptotics and convergence rates. Preprint. Available at https://arxiv.org/abs/2108.02316.Google Scholar
Favaro, S., Fortini, S. and Peluchetti, S. (2022). Neural tangent kernel analysis of shallow $ \alpha $ -stable ReLU neural networks. Preprint. Available at https://arxiv.org/abs/2206.08065.Google Scholar
Feller, W. (1971). An Introduction to Probability Theory and Its Applications, Vol. 2. John Wiley, New York.Google Scholar
Fortuin, V. (2021). Priors in Bayesian deep learning: a review. Preprint. Available at https://arxiv.org/abs/2105.06868.Google Scholar
Fortuin, V. (2021). Bayesian neural network priors revisited. Preprint. Available at https://arxiv.org/abs/2102.06571.Google Scholar
Ghosal, S. and van der Vaart, A. (2017). Fundamentals of Nonparametric Bayesian Inference. Cambridge University Press.Google Scholar
Ghosh, S., Yao, J. and Doshi-Velez, F. (2018). Structured variational learning of Bayesian neural networks with horseshoe priors. In Proc. 35th International Conference on Machine Learning (PMLR 80), eds J. Dy and A. Krause, Proceedings of Machine Learning Research, pp. 1744–1753.Google Scholar
Ghosh, S., Yao, J. and Doshi-Velez, F. (2019). Model selection in Bayesian neural networks via horseshoe priors. J. Mach. Learning Res. 20, 1–46.Google Scholar
Glorot, X. and Bengio, Y. (2010). Understanding the difficulty of training deep feedforward neural networks. J. Mach. Learning Res. 9, 249–256.Google Scholar
Gurbuzbalaban, M., Simsekli, U. and Zhu, L. (2021). The heavy-tail phenomenon in SGD. In Proc. 38th International Conference on Machine Learning (PMLR 139), eds M. Meila and T. Zhang, Proceedings of Machine Learning Research, pp. 3964–3975.Google Scholar
He, K., Zhang, X., Ren, S. and Sun, J. (2015). Delving deep into rectifiers: surpassing human-level performance on ImageNet classification. In Proc. 2015 IEEE International Conference on Computer Vision, Institute of Electrical and Electronics Engineers, pp. 1026–1034.CrossRefGoogle Scholar
Hodgkinson, L. and Mahoney, M. (2021). Multiplicative noise and heavy tails in stochastic optimization. In Proc. 38th International Conference on Machine Learning (PMLR 139), eds M. Meila and T. Zhang, Proceedings of Machine Learning Research, pp. 4262–4274.Google Scholar
Jacot, A., Hongler, C. and Gabriel, F. (2018). Neural tangent kernel: convergence and generalization in neural networks. In Advances in Neural Information Processing Systems 31 (NeurIPS 2018), Neural Information Processing Systems Foundation, San Diego, CA, pp. 8580–8589.Google Scholar
Jantre, S., Bhattacharya, S. and Maiti, T. (2021). Layer adaptive node selection in Bayesian neural networks: statistical guarantees and implementation details. Preprint. Available at https://arxiv.org/abs/2108.11000.Google Scholar
Kallenberg, O. (2002). Foundations of Modern Probability. Springer, Cham.Google Scholar
Kallenberg, O. (2005). Probabilistic Symmetries and Invariance Principles. Springer, New York.Google Scholar
Kallenberg, O. (2017). Random Measures, Theory and Applications Vol. 1. Springer, Cham.Google Scholar
Kuelbs, J. (1973). A representation theorem for symmetric stable processes and stable measures on H . Z. Wahrscheinlichkeitsth. 26, 259–271.Google Scholar
Lee, H., Yun, E., Yang, H. and Lee, J. (2022). Scale mixtures of neural network Gaussian processes. In Proc. 10th International Conference on Learning Representations (ICLR 2022). Available at https://openreview.net/forum?id=YVPBh4k78iZ.Google Scholar
Lee, J. (2018). Deep neural networks as Gaussian processes. In Proc. 6th International Conference on Learning Representations (ICLR 2018). Available at https://openreview.net/forum?id=B1EA-M-0Z.Google Scholar
Lee, J. (2020). Finite versus infinite neural networks: an empirical study. In Advances in Neural Information Processing Systems 33 (NeurIPS 2020), Neural Information Processing Systems Foundation, San Diego, CA, pp. 15156–15172.Google Scholar
Lee, J., Xiao, L., Schoenholz, S. S., Bahri, Y., Novak, R., Sohl-Dickstein, J. and Pennington, J. (2019). In Advances in Neural Information Processing Systems 32 (NeurIPS 2019), Neural Information Processing Systems Foundation, San Diego, CA, pp. 8570–8581.Google Scholar
Louizos, C., Ullrich, K. and Welling, M. (2017). Bayesian compression for deep learning. In Advances in Neural Information Processing Systems 30 (NIPS 2017), Neural Information Processing Systems Foundation, San Diego, CA, pp. 3288–3298.Google Scholar
Martin, C. and Mahoney, M. (2019). Traditional and heavy tailed self regularization in neural network models. In Proc. 36th International Conference on Machine Learning (PMLR 97), eds K. Chaudhuri and R. Salakhutdinov, Proceedings of Machine Learning Research, pp. 4284–4293.Google Scholar
Martin, C. H. and Mahoney, M. W. (2020). Heavy-tailed universality predicts trends in test accuracies for very large pre-trained deep neural networks. In Proc. 2020 SIAM International Conference on Data Mining (SDM), Society for Industrial and Applied Mathematics, Philadelphia, PA, pp. 505–513.Google Scholar
Matthews, A. G. de G. (2018). Gaussian process behaviour in wide deep neural networks. In Proc. 6th International Conference on Learning Representations (ICLR 2018). Available at https://openreview.net/forum?id=H1-nGgWC-.Google Scholar
Matthews, A. G. de G., Hron, J., Turner, R. E. and Ghahramani, Z. (2017). Sample-then-optimize posterior sampling for Bayesian linear models. In NeurIPS Workshop on Advances in Approximate Bayesian Inference. Available at http://approximateinference.org/2017/accepted/MatthewsEtAl2017.pdf.Google Scholar
Neal, R. M. (1996). Bayesian Learning for Neural Networks. Springer, Berlin, Heidelberg.Google Scholar
Novak, R. (2019). Bayesian deep convolutional networks with many channels are Gaussian processes. In Proc. 7th International Conference on Learning Representations (ICLR 2019). Available at https://openreview.net/forum?id=B1g30j0qF7.Google Scholar
Ober, S. W. and Aitchison, L. (2021). Global inducing point variational posteriors for Bayesian neural networks and deep Gaussian processes. In Proc. 38th International Conference on Machine Learning (PMLR 139), eds M. Meila and T. Zhang, Proceedings of Machine Learning Research, pp. 8248–8259.Google Scholar
Pitman, E. (1968). On the behaviour of the characteristic function of a probability distribution in the neighbourhood of the origin. J. Austral. Math. Soc. 8, 423–443.Google Scholar
Roberts, D. A., Yaida, S. and Hanin, B. (2022). The Principles of Deep Learning Theory. Cambridge University Press.CrossRefGoogle Scholar
Royden, H. L. and Fitzpatrick, P. (2010). Real Analysis, 4th edn. Macmillan, New York.Google Scholar
Samorodnitsky, G. and Taqqu, M. (1994). Stable Non-Gaussian Random Processes: Stochastic Models with Infinite Variance. Chapman and Hall, Boca Raton, FL.Google Scholar
Shanbhag, D. N. and Sreehari, M. (1977). On certain self-decomposable distributions. Z. Wahrscheinlichkeitsth. 38, 217–222.Google Scholar
Tsuchida, R., Roosta, F. and Gallagher, M. (2019). Richer priors for infinitely wide multi-layer perceptrons. Preprint. Available at https://arxiv.org/abs/1911.12927.Google Scholar
Wainwright, M. J. and Simoncelli, E. P. (1999). Scale mixtures of Gaussians and the statistics of natural images. In Advances in Neural Information Processing Systems 12 (NIPS 1999), MIT Press, pp. 855–861.Google Scholar
Wenzel, F. (2020). How good is the Bayes posterior in deep neural networks really? Preprint. Available at https://arxiv.org/abs/2002.02405.Google Scholar
Yang, G. (2019). Wide feedforward or recurrent neural networks of any architecture are Gaussian processes. In Advances in Neural Information Processing Systems 32 (NeurIPS 2019), Neural Information Processing Systems Foundation, San Diego, CA, pp. 9947–9960.Google Scholar