Hostname: page-component-7dd5485656-wjfd9 Total loading time: 0 Render date: 2025-10-31T06:40:57.359Z Has data issue: false hasContentIssue false
  • English
  • Français

Improved queue-size scaling for input-queued switches via graph factorization

Part of: Special processes Graph theory Computer system organization Operations research and management science

Published online by Cambridge University Press:  24 September 2020

Jiaming Xu Open the ORCID record for Jiaming Xu [Opens in a new window]  and
Yuan Zhong
Jiaming Xu*
Affiliation:
Fuqua School of Business, Duke University
Yuan Zhong*
Affiliation:
Booth School of Business, University of Chicago
*
*Postal address: 100 Fuqua Drive, Durham, NC 27708, USA. Email: jx77@duke.edu
**Postal address: 5807 South Woodlawn Ave, Chicago, IL 60637, USA. Email: yuan.zhong@chicagobooth.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper studies the scaling of the expected total queue size in an 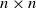$n\times n$ input-queued switch, as a function of both the load 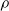$\rho$ and the system scale n. We provide a new class of scheduling policies under which the expected total queue size scales as 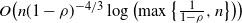$O\big( n(1-\rho)^{-4/3} \log \big(\!\max\big\{\frac{1}{1-\rho}, n\big\}\big)\big)$, over all n and 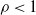$\rho<1$, when the arrival rates are uniform. This improves on the best previously known scalings in two regimes: 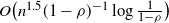$O\big(n^{1.5}(1-\rho)^{-1} \log \frac{1}{1-\rho}\big)$ when 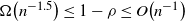$\Omega\big(n^{-1.5}\big) \le 1-\rho \le O\big(n^{-1}\big)$ and 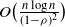$O\big(\frac{n\log n}{(1-\rho)^2}\big)$ when 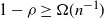$1-\rho \geq \Omega(n^{-1})$. A key ingredient in our method is a tight characterization of the largest k-factor of a random bipartite multigraph, which may be of independent interest.

Keywords

Input-queued switchqueue-size scalinggraph factorization

MSC classification

Primary: 60K25: Queueing theory
Secondary: 05C70: Factorization, matching, partitioning, covering and packing 68M20: Performance evaluation; queueing; scheduling 90B36: Scheduling theory, stochastic

Information

Type
Original Article
Information
Advances in Applied Probability , Volume 52 , Issue 3 , September 2020 , pp. 798 - 824
Check for updates
Copyright
© Applied Probability Trust 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Akiyama, J. and Kano, M. (2011). Factors and Factorizations of Graphs: Proof Techniques in Factor Theory. Springer, Berlin, Heidelberg.CrossRefGoogle Scholar
Alizadeh, M.et al. (2013). pFabric: Minimal near-optimal datacenter transport. SIGCOMM Comput. Commun. Rev. 43, 435–446.CrossRefGoogle Scholar
Chowdhury, M., Zhong, Y. and Stoica, I. (2014). Efficient coflow scheduling with Varys. In Proc. ACM SIGCOMM 2014, Association for Computing Machinery, New York, pp. 443–454.CrossRefGoogle Scholar
Chung, F. (2006). Complex Graphs and Networks. American Mathematical Society, Providence, RI.CrossRefGoogle Scholar
Csaba, B. (2007). Regular spanning subgraphs of bipartite graphs of high minimum degree. Electron. J. Combinatorics 14, N21.10.37236/1022CrossRefGoogle Scholar
Dai, J. G. and Prabhakar, B. (2000). The throughput of switches with and without speed-up. In Proc. IEEE INFOCOM 2000, Tel Aviv, Israel, pp. 556–564.Google Scholar
De Veciana, G., Lee, T. and Konstantopoulos, T. (2001). Stability and performance analysis of networks supporting elastic services. IEEE/ACM Trans. Networking 9, 2–14.CrossRefGoogle Scholar
Ford, L. R. and Fulkerson, D. R. (1956). Maximal flow through a network. Canad. J. Math. 8, 399–404.10.4153/CJM-1956-045-5CrossRefGoogle Scholar
Gale, D.et al. (1957). A theorem on flows in networks. Pacific J. Math. 7, 1073–1082.CrossRefGoogle Scholar
Harrison, J. M. (2000). Brownian models of open processing networks: canonical representation of workload. Ann. Appl. Prob. 10, 75–103. (Correction: 13 (2003), 390–393.)CrossRefGoogle Scholar
Hassin, R. and Zemel, E. (1988). Probabilistic analysis of the capacitated transportation problem. Math. Operat. Res. 13, 80–89.CrossRefGoogle Scholar
Kelly, F. P. and Williams, R. J. (2004). Fluid model for a network operating under a fair bandwidth-sharing policy. Ann. Appl. Prob. 14, 1055–1083.CrossRefGoogle Scholar
Keslassy, I. and McKeown, N. (2001). Analysis of scheduling algorithms that provide 100% throughput in input-queued switches. Proc. Annual Allerton Conference on Communication, Control and Computing 39, 593–602.Google Scholar
Leonardi, E., Mellia, M., Neri, F. and Marsan, M. A. (2001). Bounds on average delays and queue size averages and variances in input queued cell-based switches. In Proc. IEEE INFOCOM 2001, Anchorage, AK, pp. 1095–1103.CrossRefGoogle Scholar
Lin, W. and Dai, J. G. (2005). Maximum pressure policies in stochastic processing networks. Operat. Res. 53, 197–218.Google Scholar
Maguluri, S. T. and Srikant, R. (2016). Heavy traffic queue length behavior in a switch under the Maxweight algorithm. Stoch. Systems 6, 211–250.CrossRefGoogle Scholar
McKeown, N., Anantharam, V. and Walrand, J. (1996). Achieving 100% throughput in an input-queued switch. In Proc. IEEE INFOCOM ’96, San Francisco, CA, pp. 296–302.CrossRefGoogle Scholar
Neely, M., Modiano, E. and Cheng, Y. S. (2007). Logarithmic delay for $n\times n$ packet switches under the cross-bar constraint. IEEE/ACM Trans. Networking 15, 657–668.CrossRefGoogle Scholar
Perry, J.et al. (2014). Fastpass: A centralized “zero-queue” datacenter network. In Proc. ACM SIGCOMM 2014, Association for Computing Machinery, New York, pp. 307–318.10.1145/2619239.2626309CrossRefGoogle Scholar
Plummer, M. D. (2007). Graph factors and factorization: 1985–2003: a survey. Discrete Math. 307, 791–821.10.1016/j.disc.2005.11.059CrossRefGoogle Scholar
Ryser, H. J. (1957). Combinatorial properties of matrices of zeros and ones. Canad. J. Math. 9, 371–377.CrossRefGoogle Scholar
Shah, D. and Kopikare, M. (2002). Delay bounds for approximate Maximum Weight matching algorithms for input queued switches. In Proc. IEEE INFOCOM 2002, IEEE, New York, pp. 1024–1031.10.1109/INFCOM.2002.1019350CrossRefGoogle Scholar
Shah, D., Tsitsiklis, J. N. and Zhong, Y. (2011). Optimal scaling of average queue sizes in an input-queued switch: an open problem. Queueing Systems 68, 375–384.CrossRefGoogle Scholar
Shah, D., Tsitsiklis, J. N. and Zhong, Y. (2016). On queue-size scaling for input-queued switches. Stoch. Systems 6, 1–25.CrossRefGoogle Scholar
Shah, D., Walton, N. and Zhong, Y. (2014). Optimal queue-size scaling in switched networks. Ann. Appl. Prob. 24, 2207–2245.10.1214/13-AAP970CrossRefGoogle Scholar
Shamir, E. and Upfal, E. (1981). On factors in random graphs. Israel J. Math. 39, 296–302.CrossRefGoogle Scholar
Srikant, R. and Ying, L. (2014). Communication Networks: An Optimization, Control and Stochastic Networks Perspective. Cambridge University Press.Google Scholar
Stolyar, A. L. (2004). MaxWeight scheduling in a generalized switch: State space collapse and workload minimization in heavy traffic. Ann. Appl. Prob. 14, 1–53.10.1214/aoap/1075828046CrossRefGoogle Scholar
Tassiulas, L. and Ephremides, A. (1992). Stability properties of constrained queueing systems and scheduling policies for maximum throughput in multihop radio networks. IEEE Trans. Automatic Control 37, 1936–1948.10.1109/9.182479CrossRefGoogle Scholar