Hostname: page-component-76fb5796d-x4r87 Total loading time: 0 Render date: 2024-04-29T04:14:57.235Z Has data issue: false hasContentIssue false
  • English
  • Français

An extreme worst-case risk measure by expectile

Part of: Stochastic processes

Published online by Cambridge University Press:  02 April 2024

Yanlin Hu ,
Yu Chen Open the ORCID record for Yu Chen [Opens in a new window]  and
Tiantian Mao
Yanlin Hu*
Affiliation:
University of Science and Technology of China
Yu Chen*
Affiliation:
University of Science and Technology of China
Tiantian Mao*
Affiliation:
University of Science and Technology of China
*
*Postal address: Department of Statistics and Finance, IIF, School of Management, University of Science and Technology of China, Hefei 230026, Anhui, P. R. China.
*Postal address: Department of Statistics and Finance, IIF, School of Management, University of Science and Technology of China, Hefei 230026, Anhui, P. R. China.
*Postal address: Department of Statistics and Finance, IIF, School of Management, University of Science and Technology of China, Hefei 230026, Anhui, P. R. China.
Get access Rights & Permissions [Opens in a new window]

Abstract

Expectiles have received increasing attention as a risk measure in risk management because of their coherency and elicitability at the level 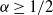$\alpha\geq1/2$. With a view to practical risk assessments, this paper delves into the worst-case expectile, where only partial information on the underlying distribution is available and there is no closed-form representation. We explore the asymptotic behavior of the worst-case expectile on two specified ambiguity sets: one is through the Wasserstein distance from a reference distribution and transforms this problem into a convex optimization problem via the well-known Kusuoka representation, and the other is induced by higher moment constraints. We obtain precise results in some special cases; nevertheless, there are no unified closed-form solutions. We aim to fully characterize the extreme behaviors; that is, we pursue an approximate solution as the level $\alpha $ tends to 1, which is aesthetically pleasing. As an application of our technique, we investigate the ambiguity set induced by higher moment conditions. Finally, we compare our worst-case expectile approach with a more conservative method based on stochastic order, which is referred to as ‘model aggregation’.

Keywords

Expectileextreme value theoryambiguityWasserstein distancemoment constraints

MSC classification

Primary: 60G70: Extreme value theory; extremal processes
Type
Original Article
Information
Advances in Applied Probability , First View , pp. 1 - 20
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on behalf of Applied Probability Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ahmad, A. A. et al. (2020). Estimation of extreme quantiles from heavy-tailed distributions in a location-dispersion regression model. Electron. J. Statist. 14, 4421–4456.CrossRefGoogle Scholar
Bartl, D., Drapeau, S. and Tangpi, L. (2020). Computational aspects of robust optimized certainty equivalents and option pricing. Math. Finance 30, 287–309.CrossRefGoogle Scholar
Bellini, F. and Bignozzi, V. (2015). On elicitable risk measures. Quant. Finance 15, 725–733.CrossRefGoogle Scholar
Bellini, F., Klar, B., Müller, A. and Rosazza-Gianin, E. (2014). Generalized quantiles as risk measures. Insurance Math. Econom. 54, 41–48.CrossRefGoogle Scholar
Bernard, C., Pesenti, S. M. and Vanduffel, S. (2022). Robust distortion risk measures. Preprint. Available at https://arxiv.org/abs/2205.08850.Google Scholar
Chen, L., He, S. and Zhang, S. (2011). Tight bounds for some risk measures, with applications to robust portfolio selection. Operat. Res. 59, 847–865.CrossRefGoogle Scholar
Chen, Z., Yu, P. and Haskell, W. B. (2019). Distributionally robust optimization for sequential decision-making. Optimization 68, 2397–2426.CrossRefGoogle Scholar
Delage, E. and Ye, Y. (2010). Distributionally robust optimization under moment uncertainty with application to data-driven problems. Operat. Res. 58, 595–612.CrossRefGoogle Scholar
Dunkel, J. and Weber, S. (2010). Stochastic root finding and efficient estimation of convex risk measures. Operat. Res. 58, 1505–1521.CrossRefGoogle Scholar
Embrechts, P., Wang, B. and Wang, R. (2015). Aggregation-robustness and model uncertainty of regulatory risk measures. Finance Stoch. 19, 763–790.CrossRefGoogle Scholar
Föllmer, H. and Schied, A. (2002). Convex measures of risk and trading constraints. Finance Stoch. 6, 429–447.CrossRefGoogle Scholar
Ghaoui, L. E., Oks, M. and Oustry, F. (2003). Worst-case value-at-risk and robust portfolio optimization: a conic programming approach. Operat. Res. 51, 543–556.CrossRefGoogle Scholar
Giesecke, K., Schmidt, T. and Weber, S. (2008). Measuring the risk of large losses. J. Investment Manag. 6, 1–15.Google Scholar
Glasserman, P. and Xu, X. (2014). Robust risk measurement and model risk. Quant. Finance 14, 29–58.CrossRefGoogle Scholar
Guo, S. and Xu, H. (2019). Distributionally robust shortfall risk optimization model and its approximation. Math. Program. 174, 473–498.CrossRefGoogle Scholar
Hu, Z. and Dali, Z. (2016). Convex risk measures: efficient computations via Monte Carlo. Available at https://ssrn.com/abstract=2758713.Google Scholar
Liu, F., Mao, T., Wang, R. and Wei, L. (2022). Inf-convolution, optimal allocations, and model uncertainty for tail risk measures. Math. Operat. Res. 47, 2494–2519.CrossRefGoogle Scholar
Mao, T., Wang, R. and Wu, Q. (2022). Model aggregation for risk evaluation and robust optimization. Preprint. Available at https://arxiv.org/abs/2201.06370.Google Scholar
Mohajerin-Esfahani, P. and Kuhn, D. (2018). Data-driven distributionally robust optimization using the Wasserstein metric: performance guarantees and tractable reformulations. Math. Program. 171, 115–166.CrossRefGoogle Scholar
Natarajan, K., Pachamanova, D. and Sim, M. (2008). Incorporating asymmetric distributional information in robust value-at-risk optimization. Manag. Sci. 54, 573–585.CrossRefGoogle Scholar
Newey, W. K. and Powell, J. L. (1987). Asymmetric least squares estimation and testing. Econometrica 55, 819–847.CrossRefGoogle Scholar
Panaretos, V. M. and Zemel, Y. (2020). An Invitation to Statistics in Wasserstein Space. Springer, Cham.CrossRefGoogle Scholar
Pesenti, S. M., Millossovich, P. and Tsanakas, A. (2016). Robustness regions for measures of risk aggregation. Dependence Modeling 4, 348–367.CrossRefGoogle Scholar
Pesenti, S. M., Wang, Q. and Wang, R. (2020). Optimizing distortion risk metrics with distributional uncertainty. Preprint. Available at https://arxiv.org/abs/2011.04889.Google Scholar
Rockafellar, R. T. and Uryasev, S. (2000). Optimization of conditional value-of-risk. J. Risk 2, 21–41.CrossRefGoogle Scholar
Shapiro, A. (2017). Distributionally robust stochastic programming. SIAM J. Optimization 27, 2258–2275.CrossRefGoogle Scholar
Villani, C. (2009). Optimal Transport: Old and New. Springer, Berlin.CrossRefGoogle Scholar
Wang, Q., Wang, R. and Wei, Y. (2020a). Distortion risk metrics on general spaces. ASTIN Bull. 50, 827–851.CrossRefGoogle Scholar
Wang, R., Wei, Y. and Willmot, G. E. (2020b). Characterization, robustness and aggregation of signed Choquet integrals. Math. Operat. Res. 45, 993–1015.CrossRefGoogle Scholar
Wiesemann, W., Kuhn, D. and Sim, M. (2014). Distributionally robust convex optimization. Operat. Res. 62, 1203–1466.CrossRefGoogle Scholar
Zhu, M. S. and Fukushima, M. (2009). Worst-case conditional value-at-risk with application to robust portfolio management. Operat. Res. 57, 1155–1168.CrossRefGoogle Scholar
Ziegel, J. F. (2016). Coherence and elicitability. Math. Finance 26, 901–918.CrossRefGoogle Scholar
Supplementary material: File

Hu et al. supplementary material

Hu et al. supplementary material
Download Hu et al. supplementary material(File)
File 1.3 MB