Hostname: page-component-89b8bd64d-9prln Total loading time: 0 Render date: 2026-05-10T05:28:27.915Z Has data issue: false hasContentIssue false
  • English
  • Français

A bootstrap algorithm for the isotropic random sphere

Part of: Nonparametric inference Stochastic processes

Published online by Cambridge University Press:  01 July 2016

Jason J. Brown
Jason J. Brown*
Affiliation:
University of Missouri—Columbia
*
* Present address: 5825 Saddle Seat Drive, Raleigh, NC 27606, USA.
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 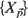be a real-valued, homogeneous, and isotropic random field indexed in 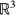. When restricted to those indices 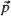with 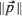, the Euclidean length of 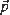, equal to r (a positive constant), then the random field resides on the surface of a sphere of radius r. Using a modified stratified spherical sampling plan (Brown (1993a)) 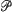on the sphere, define 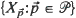to be a realization of the random process and 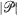to be the cardinality of 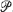. A bootstrap algorithm is presented and conditions for strong uniform consistency of the bootstrap cumulative distribution function of the standardized sample mean, 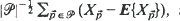, are given. We illustrate the bootstrap algorithm with global land-area data.

Keywords

BOOTSTRAPSAMPLING PLANISOTROPIC RANDOM FIELDSPHERE

MSC classification

Primary: 62G09: Resampling methods
Secondary: 60G60: Random fields

Information

Type
Stochastic Geometry and Statistical Applications
Information
Advances in Applied Probability , Volume 27 , Issue 3 , September 1995 , pp. 627 - 641
Copyright
Copyright © Applied Probability Trust 1995 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

This research was partially supported by NSF grant DMS-94.04130.

References

Brown, J. (1993a) A Finite Sampling Plan, Central Limit Theorem, and Bootstrap Algorithm for a Homogeneous and Isotropic Random Field on the 3-dimensional Sphere. Ph.D. Thesis, Department of Statistics, The University of North Carolina at Chapel Hill, Mimeo Series #2097.Google Scholar
Brown, J. (1993b) A central limit theorem for an isotropic random sphere. Adv. Appl. Prob. 27, 642–65.Google Scholar
Chung, K. L. (1974) A Course in Probability Theory, 2nd edn. Academic Press, New York.Google Scholar
Ibragimov, I. and Linnik, Y. (1971) Independent and Stationary Sequences of Random Variables. Wolters-Noordhoff, Groningen.Google Scholar
Künsch, K. (1989) The jackknife and the bootstrap for general stationary observations. Ann. Statist. 17, 1217–1241.Google Scholar
Rosenblatt, M. (1956) A central limit theorem and a strong mixing condition. Proc. Nat. Acad. Sci. USA 42, 43–47.Google Scholar
Singh, K. (1981) On the asymptotic accuracy of Efron's bootstrap. Ann. Statist. 9, 1187–1195.Google Scholar