Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Frank, Till D.
2009.
Encyclopedia of Complexity and Systems Science.
p.
5239.
Frank, Till D.
2020.
Synergetics.
p.
149.

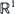 :
: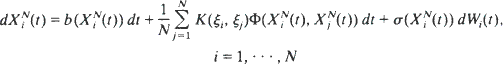
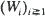 is a sequence of independent copies of the one-dimensional Brownian motion
is a sequence of independent copies of the one-dimensional Brownian motion