Hostname: page-component-76fb5796d-skm99 Total loading time: 0 Render date: 2024-04-28T17:49:43.494Z Has data issue: false hasContentIssue false
  • English
  • Français

Non-asymptotic control of the cumulative distribution function of Lévy processes

Part of: Stochastic processes Distribution theory - Probability Design of experiments

Published online by Cambridge University Press:  15 June 2022

Céline Duval  and
Ester Mariucci Open the ORCID record for Ester Mariucci [Opens in a new window]
Céline Duval*
Affiliation:
Université de Lille, CNRS, UMR 8524—Laboratoire Paul Painlevé
Ester Mariucci*
Affiliation:
Université Paris-Saclay, UVSQ, CNRS, Laboratoire de Mathématiques de Versailles
*
*Postal address: Cité Scientifique—59650 Villeneuve d’Ascq, France. Email address: celine.duval@univ-lille.fr
**Postal address: 45 Av. des États Unis, 78000 Versailles, France. Email address: ester.mariucci@uvsq.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

We propose non-asymptotic controls of the cumulative distribution function 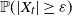$\mathbb{P}(|X_{t}|\ge \varepsilon)$ , for any 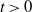$t>0$ 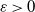, $\varepsilon>0$ and any Lévy process X such that its Lévy density is bounded from above by the density of an $\alpha$ -stable-type Lévy process in a neighborhood of the origin.

Keywords

Lévy processessmall jumpsinfinitely divisible distributions

MSC classification

Primary: 60G51: Processes with independent increments; L'evy processes 60E07: Infinitely divisible distributions; stable distributions
Secondary: 62K99: None of the above, but in this section
Type
Original Article
Information
Advances in Applied Probability , Volume 54 , Issue 3 , September 2022 , pp. 913 - 944
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of Applied Probability Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Barndorff-Nielsen, O. E. and Hubalek, F. (2008). Probability measures, Lévy measures and analyticity in time. Bernoulli 14, 764–790.CrossRefGoogle Scholar
Barndorff-Nielsen, O. E., Mikosch, T. and Resnick, S. I. (eds) (2012). Lévy Processes: Theory and Applications. Springer, New York.Google Scholar
Bertoin, J. (1996). Lévy Processes. Cambridge University Press.Google Scholar
Carpentier, A., Duval, C. and Mariucci, E. (2021). Total variation distance for discretely observed Lévy processes: a Gaussian approximation of the small jumps. Ann. Inst. H. Poincaré Prob. Statist. 57, 901–939.CrossRefGoogle Scholar
Cohen, S. and Rosinski, J. (2007). Gaussian approximation of multivariate Lévy processes with applications to simulation of tempered stable processes. Bernoulli 13, 195–210.10.3150/07-BEJ6011CrossRefGoogle Scholar
Cont, R. and Tankov, P. (2004). Financial Modelling with Jump Processes. Chapman and Hall/CRC, Boca Raton.Google Scholar
Duval, C. and Mariucci, E. (2021). Spectral-free estimation of Lévy densities in high-frequency regime. Bernoulli 27, 2649–2674.10.3150/21-BEJ1326CrossRefGoogle Scholar
Dzhaparidze, K. and Van Zanten, J. (2001). On Bernstein-type inequalities for martingales. Stoch. Process. Appl. 93, 109–117.10.1016/S0304-4149(00)00086-7CrossRefGoogle Scholar
Figueroa-López, J. E. and Houdré, C. (2009). Small-time expansions for the transition distributions of Lévy processes. Stoch. Process. Appl. 119, 3862–3889.CrossRefGoogle Scholar
Gnedenko, B. and Kolmogorov, A. (1954). Limit Distributions for Sums of Independent Random Variables. Addison-Wesley, Cambridge, MA.Google Scholar
Ishikawa, Y. (1994). Asymptotic behavior of the transition density for jump type processes in small time. Tohoku Math. J. 46, 443–456.10.2748/tmj/1178225674CrossRefGoogle Scholar
Léandre, R. (1987). Densité en temps petit d’un processus de sauts. In Séminaire de Probabilités XXI, eds Azéma, J., Mayer, P. A. and Yor, M., Springer, Berlin, Heidelberg, pp. 81–99.CrossRefGoogle Scholar
Marchal, P. (2009). Small time expansions for transition probabilities of some Lévy processes. Electron. Commun. Prob. 14, 132–142.CrossRefGoogle Scholar
Picard, J. (1997). Density in small time for Lévy processes. ESAIM Prob. Statist. 1, 357–389.CrossRefGoogle Scholar
Rosiński, J. (2007). Tempering stable processes. Stoch. Process. Appl. 117, 677–707.CrossRefGoogle Scholar
Rüschendorf, L. and Woerner, J. H. C. (2002). Expansion of transition distributions of Lévy processes in small time. Bernoulli 8, 81–96.Google Scholar