Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Hutton, J.
1980.
The recurrence and transience of two-dimensional linear birth and death processes.
Advances in Applied Probability,
Vol. 12,
Issue. 3,
p.
615.
Hutton, J.
1980.
The recurrence and transience of two-dimensional linear birth and death processes.
Advances in Applied Probability,
Vol. 12,
Issue. 03,
p.
615.
Rittgen, W.
1980.
Biological Growth and Spread.
Vol. 38,
Issue. ,
p.
98.
Klebaner, Fima C.
1989.
Linear growth in near-critical population-size-dependent multitype Galton–Watson processes.
Journal of Applied Probability,
Vol. 26,
Issue. 03,
p.
431.
Klebaner, Fima C.
1990.
Conditions for the unlimited growth in multitype population size dependent galton-watson processes.
Bulletin of Mathematical Biology,
Vol. 52,
Issue. 4,
p.
527.
Borovkov, A. A.
1992.
Lyapunov Functions and Ergodicity of Multidimensional Markov Chains.
Theory of Probability & Its Applications,
Vol. 36,
Issue. 1,
p.
1.
Durrett, Rick
1999.
Perplexing Problems in Probability.
p.
1.
Raimond, Olivier
and
Schapira, Bruno
2010.
Random walks with occasionally modified transition probabilities.
Illinois Journal of Mathematics,
Vol. 54,
Issue. 4,
Crane, Edward
Georgiou, Nicholas
Volkov, Stanislav
Wade, Andrew R.
and
Waters, Robert J.
2011.
The simple harmonic urn.
The Annals of Probability,
Vol. 39,
Issue. 6,
Popov, Serguei
Shcherbakov, Vadim
and
Volkov, Stanislav
2022.
Linear competition processes and generalized Pólya urns with removals.
Stochastic Processes and their Applications,
Vol. 144,
Issue. ,
p.
125.
B.S., Vineeth
and
Singh, Chandramani
2022.
Stability and average delay in delay tolerant networks with Poisson packet arrivals and buffered relay nodes.
Performance Evaluation,
Vol. 157-158,
Issue. ,
p.
102319.
Gómez‐Corral, Antonio
Langwade, Joshua
López‐García, Martín
and
Molina‐París, Carmen
2023.
Sufficient conditions for regularity, positive recurrence, and absorption in level‐dependent QBD processes and related block‐structured Markov chains.
Mathematical Methods in the Applied Sciences,
Vol. 46,
Issue. 6,
p.
6756.

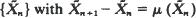 w.p.1 to move off to infinity, respectively to return to a compact set infinitely often. As an application we determine of most two-dimensional birth and death processes with rates linearly dependent on the population, whether they can escape to infinity or not.
w.p.1 to move off to infinity, respectively to return to a compact set infinitely often. As an application we determine of most two-dimensional birth and death processes with rates linearly dependent on the population, whether they can escape to infinity or not.