CONCEPTUALIZING RACE AS A CAUSAL VARIABLE

We regard the investigation of racial bias in policing as an inherently causal inquiry, albeit a notoriously difficult one. That is, researchers seek to assess whether police behavior during police–civilian encounters would have differed if the civilian had belonged to another racial group, holding constant civilian behavior and circumstances. As noted in Fryer (Reference Fryer2018), this “‘race effect’…is the proverbial ‘holy grail’—the parameter that we are all attempting to estimate but never quite do” (2). This task is distinct from the descriptive enterprise of merely documenting differential police behavior during encounters with various groups, as such disparities can arise via numerous processes that do not imply racial discrimination.^{Footnote 3}

The notion of a “causal effect of race” on an individual’s outcome is the subject of much contention in the literature on causal inference (Hernán Reference Hernán2016; Pearl Reference Pearl2018). Most notably, some have argued that this effect is undefined because race is an immutable, and hence nonmanipulable, characteristic (Holland Reference Holland1986). Others argue that an individual’s race is a complex, multifaceted treatment—a “bundle of sticks,” in the words of Sen and Wasow (Reference Sen and Wasow2016)—that affects outcomes through myriad channels, and therefore, researchers must be precise about the specific facets of race under consideration (Greiner and Rubin Reference Greiner and Rubin2011).

Our analysis avoids this debate by focusing on police–civilian encounters—that is, sightings of civilians by police—as the unit of analysis, rather than individuals. The manipulation of race is conceptualized as the counterfactual substitution of an individual with a different racial identity into the encounter, while holding the encounter’s objective context—location, time of day, criminal activity, etc.—fixed. In other words, the “treatment” in this case is the entire “bundle of sticks” encapsulating the race of the civilian—including, for example, skin tone, dialect, and clothing. We note that the credibility of causal inferences and the exact interpretation of racial discrimination in this framework will depend crucially on how the analyst defines “race.” We leave the specific operationalization in a given context to the analyst, and, in line with advice in Sen and Wasow (Reference Sen and Wasow2016), encourage scholars to carefully convey their conceptualization of race when studying this and related questions.^{Footnote 4}

By conceptualizing the treatment in this way, we avoid consideration of the perhaps implausible counterfactual of holding all features of an individual constant but for their race. While various aspects of racial identity and its close correlates may not be separable in the observed world, there exists a subset of comparable situations in which minority and majority civilians are observed by police. If this subset can be identified, or approximated through covariate adjustment, we can estimate the counterfactual police behavior that would have occurred had the civilian in question been replaced with a member of another racial group.

While our approach considers a valid counterfactual and isolates racial discrimination that occurs during police–civilian encounters, it necessarily mutes the influence of pre-encounter macroinstitutional factors, such as decisions to deploy more officers to communities of color. In keeping with the goals of prior studies in this area, our approach holds such contextual features constant, allowing us to ask whether an encounter would have unfolded differently had it involved a civilian of differing race. But even if no such difference exists within encounters, law enforcement strategies adopted before encounters occur could still produce racially biased policing. We caution readers to keep this scope condition in mind.

PRIOR RESEARCH ON RACIAL BIAS IN POLICING

Race-based selection into policing data has been previously noted, and some scholars have devised research designs in an attempt to sidestep this issue. Grogger and Ridgeway (Reference Grogger and Ridgeway2006), for example, leverage the so-called “veil of darkness” strategy, comparing patterns in traffic stops that occur before and after sunset under the logic that the race of the driver is plausibly hidden to police officers after dark. In this way, the study aims to identify a sample of police–civilian interactions that were initiated in a race-blind manner. Similarly, West (Reference West2018) examines data on police responses to traffic incidents, arguing that whether a co-racial officer responds to a motorist’s unanticipated accident is as-if random. If the assumptions in these studies hold, concerns over race-based sample selection are greatly alleviated.

These attempts to mitigate race-based selection remain rare, as most empirical studies in this literature focus nearly exclusively on mitigating the more familiar problem of omitted variable bias. For example, Fryer (Reference Fryer2019) (detailed below), a study of racial bias in police violence, estimates discrimination using data on police–civilian encounters via multivariate regressions that control for a host of observables relating to civilians, officers, and circumstance. In a related article, the author asserts that “regression can recover the ‘race effect’ if race is ‘as good as randomly assigned,’ conditional on the covariates” (Fryer Reference Fryer2018, 2). Fryer (Reference Fryer2019) claims to find evidence of bias in sublethal force but none in lethal encounters.

A related study, Johnson et al. (Reference Johnson, Tress, Burkel, Taylor and Cesario2019), attempts to estimate racial bias in police shootings. Examining only positive cases in which fatal shootings occurred, they find that the majority of shooting victims are white and conclude from this that no antiminority bias exists. Knox and Mummolo (Reference Knox and Mummolo2020) show that this conclusion rests on the erroneous assumption that police encounter minority and white civilians in equal number.

Prior work has also examined racial bias in traffic enforcement, such as Ridgeway (Reference Ridgeway2006) which employs propensity score weighting when estimating racial bias in traffic stops in Oakland, CA. The analysis examines outcomes including citations, stop duration, and the decision to search cars. The study claims this reweighting strategy can recover “the causal effect of race” (9) on poststop outcomes. In general, the analysis finds little evidence of racial bias on most outcomes, with the exception of stop duration. Antonovics and Knight (Reference Antonovics and Knight2009) use data on traffic citations from the Boston Police Department to estimate the probability that a ticketed driver was searched, controlling for driver attributes such as age, race, and gender as well as neighborhood traits. They interpret the coefficient on an indicator of whether the officer and ticketed driver are of different races as an estimate of “racial profiling based on prejudice,” as opposed to statistical discrimination (167). The claim is implicitly causal: some share of searches among racially mismatched driver–officer pairs would not have occurred had the driver belonged to another racial group.

The above examples represent a mere fraction of a decades-long, multidisciplinary effort to quantify the degree to which police discriminate against civilians of color [see Atiba Goff and Kahn (Reference Atiba Goff and Kahn2012), Fridell (Reference Fridell2017), and Ridgeway and MacDonald (Reference Ridgeway and MacDonald2010) for more extensive reviews of this empirical literature]. We highlight these specific examples because they all contain several common features that are central to our critique. For one, these studies analyze data that fail to capture the unseen selective process through which police come to engage civilians, a process that prior work shows is function of civilian race (Gelman, Fagan, and Kiss Reference Gelman, Fagan and Kiss2007). In this way, these studies all fail to account for the impact of race on the composition of the sample under study. As we show below, failing to account for this undocumented first stage of the police–civilian interaction will lead to statistical bias, even if the goal is to estimate the effect of suspect race within the sample of individuals who appear in police data and, in many cases, even with a “complete” set of control variables that render civilian race as-if randomly assigned to police encounters.

Second, the aforementioned studies, despite making at least implicitly causal claims, leave ambiguous the precise quantity of interest—whether it be the average treatment effect (ATE) of race in all encounters; the average treatment effect among the subset of encounters appearing in police data because a stop was made (ATE_M=1), which differs tremendously from the ATE; or the markedly more restrictive and difficult-to-interpret controlled direct effect among the same subset (CDE_M=1, defined below). While studies commonly discuss omitted variable bias and attendant assumptions, they rarely discuss the additional assumptions necessary to identify specific causal quantities of interest. As a result, readers are unable to assess the adequacy of research designs and estimators, rendering the interpretation and policy relevance of much prior work unclear.

CLARIFYING THE EFFECT OF CIVILIAN RACE: NOTATION, ESTIMANDS, ASSUMPTIONS, AND EXISTING APPROACHES

Researchers and policymakers examining the effects of racially biased policing are nominally interested in the relationship between two variables: the race of the civilian involved in encounter i, which we operationalize through their minority status D _i ∈ {0, 1}, and consequent police behavior Y _i ∈ {0, 1}. However, analyses of administrative data on police–civilian encounters inherently involve a mediating variable that may be affected by race: whether an individual is stopped by police, which we denote M _i. The causal ordering of these variables is depicted in the directed acyclic graph (DAG) in Figure 1. We note that analysts often possess rich contextual information about the objective context of the encounter, such as its location and time, which may relate to all of the above. We denote these covariates collectively as X _i. However, administrative data invariably fail to capture unobservable subjective aspects of the encounter, U _i, such as an officer’s suspicion or sense of threat.

FIGURE 1. Directed Acyclic Graph of Racial Discrimination in the Use of Force by Police

Notes: Observed X is left implicit; these covariates may be causally prior to any subset of D, M, and Y.

As a motivating example, we consider the challenge of estimating racial bias in police violence as recently attempted in Fryer (Reference Fryer2019). We ground our analysis in the potential outcomes framework (Rubin Reference Rubin1974) often used in the study of causal mediation (Imai et al. Reference Imai, Keele, Tingley and Yamamoto2011; Pearl Reference Pearl2001). The potential mediator M _i(d) represents whether encounter i would have resulted in a stop if the civilian were of race d. Similarly, the potential outcome Y _i(d, m) represents whether force would have been used in encounter i if the civilian were of race d and the mediating variable were m. The observed mediator and outcome can be written in terms of these potential values as ${M_i} = {M_i}\left( {{D_i}} \right) = \sum\limits_d {{M_i}\left( d \right)1\left\{ {{D_i} = d} \right\}}$ and $\eqalign{Y_i} = {Y_i}\left( {{D_i},{M_i}\left( {{D_i}} \right)} \right) = \sum\limits_d {\sum\limits_m {{Y_i}\left( {d,m} \right)1\left\{ {{D_i} = d,{M_i} = m} \right\}} }$ , respectively. For any individual encounter, the (unobservable) causal effect of civilian race is the difference in potential force if the civilian were a minority and stopped as if they were a minority, versus if they were white and stopped accordingly, Y _i(1, M _i(1)) − Y _i(0, M _i(0)).

This notation implicitly makes the stable unit treatment value assumption (SUTVA, Rubin Reference Rubin1990). “Stability” is of particular note: this stipulates that finer racial gradations must not affect the way that officers behave, above and beyond any differences between the broad binary categories D _i = 0 and D _i = 1. SUTVA also requires that each encounter is unaffected by a civilian’s race in other encounters; this might be violated if, for example, groups of individuals are stopped simultaneously.

Traditionally, analysts use data on stopped individuals to study bias by computing the difference in violence rates between stopped minority and white civilians, while controlling for observable differences between these two sets of encounters. We term this the “naïve estimator,” $\hat{\Delta }$ , and it can be written as follows:

(1) $$\hat{\Delta } = \overline {{Y_i}|{D_i} = 1,{M_i} = 1} - \overline {{Y_i}|{D_i} = 0,{M_i} = 1} ,$$

where conditioning on possible treatment-outcome confounders, X _i, is left implicit. Assuming the analyst has correctly measured and specified all such confounders, $\hat{\Delta }$ may appear entirely reasonable at the first glance. However, without further assumptions, this quantity will have no causal interpretation so long as the treatment affects the mediator (i.e., civilian race affects whether officers detain a civilian). As we show below, this is because treated encounters (with minority civilians) that result in a stop (M _i = 1) will not be comparable to those with stopped control (majority) civilians. As a simple example, suppose officers exhibited racial bias as follows: they detain white civilians if they observe them committing a serious crime (such as assault, potentially warranting the use of force) but detain nonwhite civilians regardless of observed behavior. When this is true, comparing stopped white and nonwhite civilians amounts to comparing fundamentally different groups. The analyst will observe force used against a greater proportion of stopped white civilians because of the differential physical threat they pose to officers.^{Footnote 5} Under the traditional approach, the analyst would naïvely conclude that antiwhite bias exists, yielding an erroneous portrait of racial discrimination in the use of force.

To formalize the limitations of the naïve estimator, we begin by partitioning the population into principal strata with respect to the mediator (Frangakis and Rubin Reference Frangakis and Rubin2002; VanderWeele Reference VanderWeele2011). That is, we conceptualize police–civilian encounters in terms of four latent classes within which M _i(1) and M _i(0) are constant. The general approach of principal stratification has proven useful for clarifying and bounding quantities of interest in areas ranging from instrumental variables (Angrist, Imbens, and Rubin Reference Angrist, Imbens and Rubin1996; Balke and Pearl Reference Balke and Pearl1997) to the closely related “truncation by death” problem (Rubin Reference Rubin2000; Zhang and Rubin Reference Zhang and Rubin2003).

These principal strata include “always-stop” encounters in which M _i(0) = M _i(1) = 1, as well as stops that discriminate against racial minorities (“racial stops”) in which M _i(1) = 1 but M _i(0) = 0. Always-stop encounters may be conceptualized as relatively severe scenarios, such as violent crimes in progress, in which officers have no choice but to intervene regardless of civilian race. In contrast, previous work has identified certain behaviors, such as “furtive movements” (Gelman, Fagan, and Kiss Reference Gelman, Fagan and Kiss2007; Goel, Rao, and Shroff Reference Goel, Rao and Shroff2016), that appear to be acted on selectively by officers based on the race of suspects. “Never-stop” encounters, where M _i(0) = M _i(1) = 0, are situations in which civilians appear inconspicuous and would not be stopped, regardless of race. There also may be antiwhite racial encounters, in which M _i(1) = 0 but M _i(0) = 1, though we believe these to be rare to nonexistent (discussed further below). Figure 2 shows encounters appearing in police records (principal strata for which M _i(D _i) = 1) are not comparable across civilian races. Minority police–civilian encounters that result in a stop are a mixture of “always-stop” and “antiminority racial stop” encounters, while encounters with white civilians that result in a stop are a combination of “always-stop” and “antiwhite racial stop” encounters. These are fundamentally different groups, and without further assumptions, comparisons of rates of violence between them using the naïve estimator will be statistically biased.

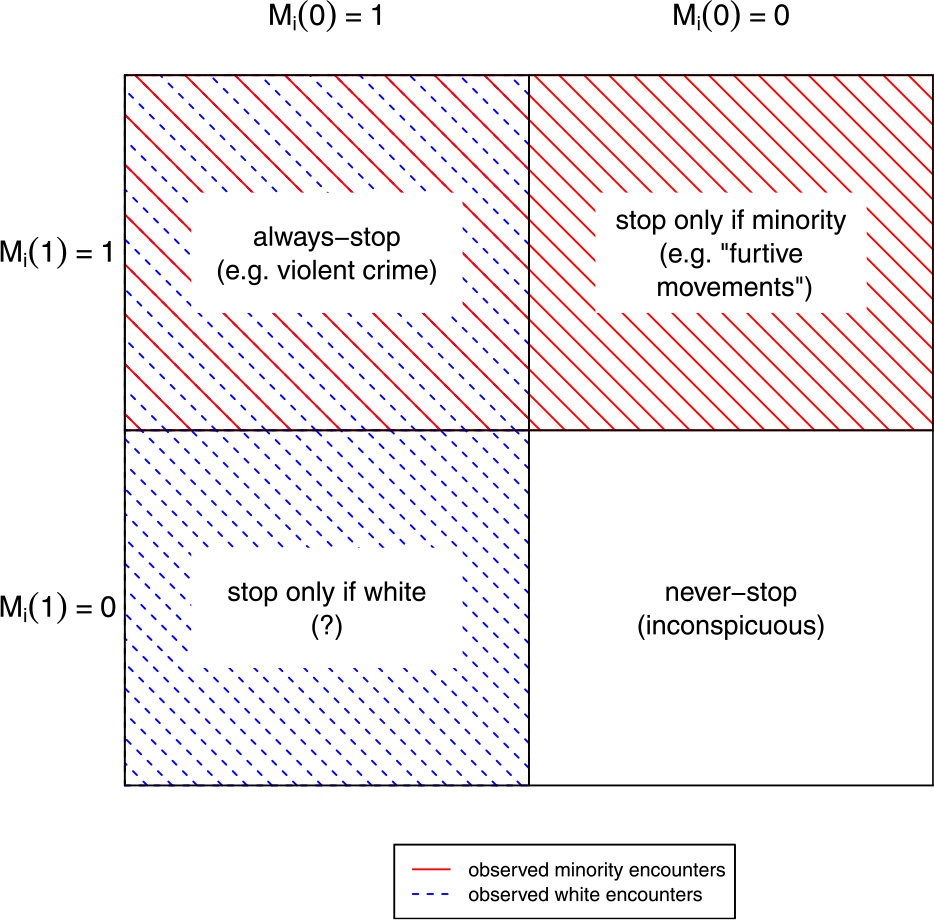
FIGURE 2. Principal Strata and Observed Police–Civilian Encounters

Notes: The figure displays the four principal strata that comprise police–civilian encounters based on how the mediator M (whether a civilian is stopped by police) responds to treatment D (whether the civilian is a racial minority). Minorities in the “always stop” and anti-minority racial stop strata, highlighted in red, are stopped by police and, thus, appear in police administrative data. Likewise, white civilians in the “always-stop” and anti-white racial stop strata, highlighted in blue, appear in police data. “Never stop” encounters are unobserved. Because white and nonwhite encounters are drawn from different principal strata, the two groups are incomparable and estimates of causal quantities using observed encounters will be statistically biased absent additional assumptions.

To state this more formally, note that the naïve estimator recovers the weighted combination of violence rates in observed principal strata:

(2) $$\eqalignb{	 {\mathbb{E}}\left[ {\hat{\Delta }} \right] = {\mathbb{E}}\left[ {{Y_i}|{D_i} = 1,{M_i} = 1} \right] - {\mathbb{E}}\left[ {{Y_i}|{D_i} = 0,{M_i} = 1} \right] \cr 	 = {\mathbb{E}}\left[ {{Y_i}\left( {1,1} \right)|{D_i} = 1,{M_i}\left( 1 \right) = 1,{M_i}\left( 0 \right) = 1} \right]\Pr \left( {{M_i}\left( 0 \right) {= 1|{D_i} = 1,{M_i}\left( 1 \right) = 1} {\right) + {\mathbb{E}}\left[ {{Y_i}\left( {1,1} \right)|{D_i} = 1,{M_i}\left( 1 \right) {= 1,{M_i}\left( 0 \right) = 0} {\right]\Pr \left( {{M_i}\left( 0 \right) = 0|{D_i} = 1,{M_i}\left( 1 \right) = 1} \right) {- {\mathbb{E}}\left[ {{Y_i}\left( {0,1} \right)|{D_i} = 0,{M_i}\left( 1 \right) = 1,{M_i}\left( 0 \right) = 1} \right]\Pr \left( {{M_i}\left( 1 \right) {= 1|{D_i} = 0,{M_i}\left( 0 \right) = 1} {\right) \cr - {\mathbb{E}}\left[ {{Y_i}\left( {0,1} \right)|{D_i} = 0,{M_i}\left( 1 \right) {= 0,{M_i}\left( 0 \right) = 1} {\right]\Pr \left( {{M_i}\left( 1 \right) = 0|{D_i} = 0,{M_i}\left( 0 \right) = 1} \right). \cr}\quad$$

In equation (2), the first term is the average rate of force applied during encounters with racial minorities of the always-stop stratum, while the second term deals with minorities in the anti–minority racial-stop stratum. The third and fourth terms are the average violence rates among white civilian encounters in the always-stop and antiwhite racial stop strata. Importantly, principal strata are not fully observable without further assumptions, and they exist even after conditioning on X _i: for any particular minority stop, it is fundamentally impossible to know with certainty whether a white civilian would have been stopped in identical circumstances. In sum, the naïve estimator compares groups with different potential outcomes, and because these groups are unobservable, the resulting bias is difficult to address.

A central quantity of interest in the study of policing bias is the average treatment effect of race, ${\rm{ATE}} = {\mathbb{E}}\left[ {{Y_i}\left( {1,{M_i}\left( 1 \right)} \right) - {Y_i}\left( {0,{M_i}\left( 0 \right)} \right)} \right]$ —the extent to which civilians of color face greater risk of police violence than white civilians because of their race. The ATE considers both reported and unreported encounters, and it captures two related phenomena: first, whether members of the minority are differentially stopped; and second, if they are differentially subject to violence. However, police administrative records contain data only on reported encounters, meaning that this quantity cannot be estimated solely with police administrative data without untenable assumptions. The ATE can be restated as follows:

(3) $$\eqalign{ 	 {\rm{ATE}} = {\mathbb{E}}\left[ {{Y_i}\left( {1,{M_i}\left( 1 \right)} \right)} \right] - {\mathbb{E}}\left[ {{Y_i}\left( {0,{M_i}\left( 0 \right)} \right)} \right] \cr 	 \quad\quad\quad= \sum\limits_d {\sum\limits_m {\sum\limits_{m'} {\left( {{\mathbb{E}}\left[ {{Y_i}\left( {1,{M_i}\left( 1 \right)} \right) - {Y_i}\left( {0,{M_i}\left( 0 \right)} \right)|{D_i} = d,{M_i}\left( 1 \right) = m,{M_i}\left( 0 \right) = m\prime } \right]} \right.} } } \cr 	 \left. { \hskip -25pt\times \Pr \left( {{D_i} = d,{M_i}\left( 1 \right) = m,{M_i}\left( 0 \right) = m\prime } \right)} \right), \cr}$$

where the second line illustrates how it sums over the principal strata depicted in Figure 2, taking into account the number of minority and white civilians in each strata (the probabilities) and the local average treatment effects for each group (the expectations). In Online Appendices A.1–A.4, we use these quantities to derive bias and nonparametric sharp bounds.

No data are available for “never-stop” encounters, those with M _i(1) = M _i(0) = 0. Moreover, racial-stop encounters, with M _i(1) = 1 and M _i(0) = 0, are only recorded for minority civilians. However, consistent with Nyhan, Skovron, and Titiunik (Reference Nyhan, Skovron and Titiunik2017), we show in Online Appendix A.6 that the ATE can be point identified if researchers collected two additional numbers: the count of total minority and white encounters, within levels of covariates X where applicable—a point we discuss further in our recommendations for future research.^{Footnote 6}

Because “never-stop” encounters are unobserved in current data sources, researchers seeking to understand the role of race in police behavior have, at least implicitly, focused on more narrowly defined estimands.^{Footnote 7} Studies commonly restrict analysis to the subset of reported encounters, that is, they seek to estimate effects among those stopped by police, ATE_M=1. In contrast to the ATE, this estimand is by definition not concerned with unreported white encounters that would have escalated to a stop if the involved civilian was a minority. (The same is true for unreported black encounters that would have escalated if the involved civilian was white, to the extent that this group exists.) Formally, this quantity is given by the following equation:

(4) $${\rm{AT}}{{\rm{E}}_{M = 1}} = {\mathbb{E}}\left[ {{Y_i}\left( {1,{M_i}\left( 1 \right)} \right)|{M_i} = 1} \right] - {\mathbb{E}}\left[ {{Y_i}\left( {0,{M_i}\left( 0 \right)} \right)|{M_i} = 1} \right].$$

Relatedly, analysts may seek to causally attribute the number of minority stops in which force would not have been used if the individual in question had been white (Yamamoto Reference Yamamoto2012). This value is proportional to the conditional average treatment effect among the treated (i.e., minority) stops, which can be written as follows:

(5) $${\hskip -58pt\rm{AT}}{{\rm{T}}_{M = 1}} = {\mathbb{E}}\left[ {{Y_i}\left( {1,{M_i}\left( 1 \right)} \right)|{D_i} = 1,{M_i} = 1} \right] - {\mathbb{E}}\left[ {{Y_i}\left( {0,{M_i}\left( 0 \right)} \right)|{D_i} = 1,{M_i} = 1} \right].$$

While the average treatment effects are of obvious policy importance, they are not the only quantity that researchers might seek to estimate. A closely related estimand is the controlled direct effect among the subset of reported encounters, ${\rm{CD}}{{\rm{E}}_{M = 1}} = {\mathbb{E}}\left[ {{Y_i}\left( {1,1} \right)|{M_i} = 1} \right] - {\mathbb{E}}\left[ {{Y_i}\left( {0,1} \right)|{M_i} = 1} \right]$ . This estimand differs from the ATE_M=1 in its conceptual approach to racially discriminatory stops. Where the ATE_M=1 asks whether a stop would have occurred at all if the individual were of differing race, the CDE_M=1 seeks to quantify what would have happened if the officer was forced to stop them anyway, perhaps against the officer’s will. In practice, the difference is one of interpretation—regardless of the target quantity, existing work in this domain is based on the naïve difference in reported outcomes, and the question lies in the interpretation of estimated results. We note that causal estimands in the literature are often left undefined, making it difficult to assess whether published results are intended to correspond to the ATE_M=1 or CDE_M=1 (e.g., Goel, Rao, and Shroff Reference Goel, Rao and Shroff2016; Simoiu, Corbett-Davies, and Goel Reference Simoiu, Corbett-Davies and Goel2017). In Online Appendix A.3, we discuss the CDE_M=1 at length. We show that it cannot be recovered in this setting unless analysts make the untenable assumption that no mediator-outcome confounding exists (Assumption 5, below). We refer readers to the Online Appendix for further details and focus on recovery of average treatment effects here.

Necessary Assumptions

In this subsection, we describe a number of statistical assumptions that the analyst must make for a causal study of racially biased policing when only administrative data on police–civilian interactions is available. Without these assumptions, causal quantities of interest in this substantive area cannot be identified in data.

Assumption 1 (Mandatory Reporting).Y _i(d, 0) = 0 for all i and for d ∈ {0, 1}.

We assume all encounters that escalate to the use of force also trigger a reporting requirement and are, therefore, observed in administrative data. Though there exist wide variability in data recording practices across jurisdictions, this assumption is plausible in the study of many major police departments. For example, New York Police Department (NYPD) officers are required to report a number of variables, including the specific type of force used, following each “stop, question, and frisk” encounter. Based on these and other reports, the NYPD releases detailed annual use-of-force reports (NYPD 2017). The completeness of these reports with respect to fatalities is informally enforced by standard journalistic practices which place high emphasis on documenting violent incidents (Iyengar Reference Iyengar1994). Lesser forms of force are more likely to go unreported, to be sure, but the ubiquity of surveillance cameras, cell phone cameras, and media interest in police brutality makes unobserved uses of force increasingly unlikely (Fisher and Hermann Reference Fisher and Hermann2015). We note that this assumption is implicit in all analyses of police use of force that rely on administrative data.

Assumption 2 (Mediator Monotonicity).M _i(1) ≥ M _i(0) for all i.

This assumption allows that there may be encounters in which minorities would be stopped (M _i(1) = 1) but whites would not (M _i(0) = 0), perhaps because officers racially discriminate in applying differential thresholds of “reasonable suspicion.” However, we assume that the reverse is never true: white civilians are never stopped in circumstances when their minority counterparts would be allowed to pass. This is clearly a stylized representation of a complex reality, and it would be violated if minority officers discriminate against white civilians. A violation could also occur if white civilians were more likely to be stopped by police because they appeared out of place in a predominantly black neighborhood, perhaps under the assumption that they were there to buy drugs (Gelman, Fagan, and Kiss Reference Gelman, Fagan and Kiss2007, 822). These are rare occurrences, and a robustness check in Online Appendix B.3, our reanalysis of Fryer (Reference Fryer2019) after dropping all stops based on suspicion of a drug transaction, shows substantively similar results.

Assumption 3 (Relative Nonseverity of Racial Stops). ${\mathbb{E}}\left[ {{Y_i}\left( {d,m} \right)|{D_i} = d',{M_i}\left( 1 \right) = 1,{M_i}\left( 0 \right) = 1,{X_i} = x} \right] \ge {\mathbb{E}}\left[ {{Y_i}\left( {d,m} \right)|{D_i} = d\prime ,{M_i}\left( 1 \right) = 1,{M_i}\left( 0 \right) = 0,{X_i} = x} \right]$ .

We theorize that for encounters during criminal events severe enough to warrant stopping a civilian regardless of race (i.e., “severe” or “always-stop” encounters), the use of force is as or more likely to occur than during encounters in which police have more discretion over whether to stop an individual (i.e., those in which racial discrimination in stopping can occur) in expectation. We regard this assumption, which compares violence rates within encounters that hold civilian race fixed, as highly plausible. As one hypothetical example, this assumption would imply that police are as or more likely to use force against a white civilian observed committing assault than a white civilian observed jaywalking, on average.

Assumption 4 (Treatment Ignorability).

1. (a) With respect to potential mediator M _i(d) ⫫ D _i|X _i.

2. (b) With respect to potential outcomes: Y _i(d, m) ⫫ D _i|M _i(0) = m′, M _i(1) = m″, X _i.

This states that conditional on X _i, civilian race is “as good as randomly assigned” to encounters, and officers encounter minority civilians in circumstances that are objectively no different from white encounters. Part 4(a) stipulates that the observed covariates X include the confounder W in Figure 3(a). This assumption, while strong, has become more plausible in recent years as administrative data sets have come to include a host of encounter attributes that might largely capture features observable to police which correlate with suspect race and the potential for force. However, we note that this cannot be tested, even indirectly, without data on nonstopped individuals. This assumption would be violated if neighborhoods with high shares of minority residents were more heavily policed and the analyst failed to adjust for neighborhood, for example, using fixed effects. Part 4(b) implies that, for example, if police were more heavily armed during minority-neighborhood patrols and, hence, more likely to deploy force—represented by V in Figure 3(b)—then V must be included in X. Without Assumption 4, the range of possible racial effects is so wide as to be uninformative. We also note that every study claiming to estimate racial discrimination using similar data makes this assumption, often implicitly. Our aim in this study is not to assert the plausibility of treatment ignorability, but rather to clarify that deep problems remain even if this well-known issue is somehow solved.

FIGURE 3. Violations of Assumptions

Notes: DAGs (a), (b), and (c), respectively, illustrate the violation of Assumptions 4(a), 4(b), and 5. Note that the variable U depicted in DAG (c) is almost certain to exist in the policing context, and we do not advocate the use of Assumption 5.

Bias in the Naïve Estimator

In this section, we clear up several misunderstandings about the conventional estimator, which compares reported minority stops to reported white stops (with or without covariates). First, we show that when there is any racial discrimination in detainment, selection on stops introduces unavoidable statistical bias in estimating the ATE_M=1, even when a perfect set of observed covariates renders race ignorable with respect to the potential mediator and outcomes. These results directly contradict prior assertions that “linear regression can recover the ‘race effect’ if race is ‘as good as randomly assigned,’ conditional on the covariates” (Fryer Reference Fryer2018, 2). The issue is not one of omitted variables, but rather posttreatment conditioning. Second, we clarify an important open question about the nature of this bias. Fryer (Reference Fryer2018) comments in the context of selection into arrest data that, “It is unclear how to estimate the extent of such bias or how to address it statistically” (5). Here, we derive the exact form of this bias for the ATE_M=1 and the ATT_M=1; Online Appendix A.3 does the same for the CDE_M=1. We show that the bias is always negative, resulting in naïve estimates that downplay the extent of racially discriminatory police violence. Below, we develop informative nonparametric sharp bounds that adjust the naïve estimates for the range of all possible selection bias.

Prior work on race and policing uses estimators that compare average reported outcomes in majority encounters to those in minority encounters. For simplicity of exposition, we present the special no-covariate case; Appendices A.1–A.3 derive the bias of the naïve estimator with covariate adjustment. We first refer readers to equation (1), which expresses the naïve estimator, $\hat{\Delta }$ , in terms of stratum mean potential outcomes. We demonstrate that this commonly used analytic approach fails to recover any quantity of interest under plausible assumptions. We first show that it is biased for the ATE_M=1 and ATT_M=1 unless Assumption 6 is true, and there are no racial stops. In Online Appendix A.3, we show it is also biased for the CDE_M=1 unless Assumption 5 holds—that is, always-stop encounters are identical in violence rates to racially discriminatory stops. As a result, the observed difference in means fails to recover any known causal quantity without additional, and highly implausible, assumptions.

In Online Appendix A.1, we derive the bias of $\hat{\Delta }$ when it is used to estimate ATE_M=1 under the relatively plausible Assumptions 1–4. This bias can be written as follows:

(6) $$\eqalignb{ 	 {\mathbb{E}}\left[ {\hat{\Delta }} \right] - {\rm{AT}}{{\rm{E}}_{M = 1}} \cr 	 = \left( {{\mathbb{E}}\left[ {{Y_i}\left( {1,1} \right) - {Y_i}\left( {0,1} \right)|{M_i}\left( 1 \right) = 1,{M_i}\left( 0 \right) = 1} \right]} \right. \cr 	 \left. { - {\mathbb{E}}\left[ {{Y_i}\left( {1,1} \right) - {Y_i}\left( {0,0} \right)|{M_i}\left( 1 \right) = 1,{M_i}\left( 0 \right) = 0} \right]} \right) \cr 	 \times \Pr \left( {{M_i}\left( 0 \right) = 0|{D_i} = 1,{M_i} = 1} \right)\Pr \left( {{D_i} = 1|{M_i} = 1} \right) \cr 	 - \left( {{\mathbb{E}}\left[ {{Y_i}\left( {1,1} \right)|{M_i}\left( 1 \right) = 1,{M_i}\left( 0 \right) = 1} \right]} \right. \cr 	 \left. { - {\mathbb{E}}\left[ {{Y_i}\left( {1,1} \right)|{M_i}\left( 1 \right) = 1,{M_i}\left( 0 \right) = 0} \right]} \right) \cr 	 \times \Pr \left( {{M_i}\left( 0 \right) = 0|{D_i} = 1,{M_i} = 1} \right). \cr}$$

We offer several comments on equation (6). The bias term is guaranteed to be negative, even with a perfect set of controls that render D _i ignorable, as long as there exist any racially discriminatory stops of minority civilians (or in an empirically falsified edge case).^{Footnote 8} The first term in the bias expression relates to heterogeneity in the average treatment effect, or the extent to which Y _i(1, M _i(1)) − Y _i(0, M _i(0)) differs in expectation between always-stop and racial-stop encounters—respectively, those with M _i(1) = M _i(0) = 1 and M _i(0) < M _i(1).^{Footnote 9} Bias arises because in the latter type of encounter, a white civilian would never have been detained in the first place, and hence force would never have been used—that is, ${\mathbb{E}}\left[ {{Y_i}\left( {0,0} \right)|{D_i} = 1,{M_i}\left( 1 \right) = 1,{M_i}\left( 0 \right) = 0} \right] = 0$ . Estimating the average potential outcomes of this group using stopped white civilians introduces unavoidable bias that the analyst cannot hope to eliminate simply by adding additional covariates to the estimating model. The second term is related to the difference in baseline violence rates between always-stop encounters and racially discriminatory stops; this term also vanishes if there are no racial stops.

Can the naïve estimator be rehabilitated by simply redefining the quantity of interest? In Online Appendices A.2–A.3, we show that the answer is no. The structure of the bias when $\hat{\Delta }$ is used to estimate the ATT_M=1 is simpler but leads to substantively identical conclusions: the naïve estimator is biased unless there are no racial stops. We show that bias for the ATT_M=1 is given by ${\mathbb{E}}\left[ {\hat{\Delta }} \right] - {\rm{AT}}{{\rm{T}}_{M = 1}} = - {\mathbb{E}}\left[ {{Y_i}\left( {0,1} \right)|{M_i}\left( 1 \right) = 1,{M_i}\left( 0 \right)= 1} \right]\Pr \left( {{M_i}\left( 0 \right) = 0|{M_i}\left( 1 \right) = 1} \right)$ . While the identifying assumptions for the CDE_M=1 are slightly weaker, they are nonetheless wholly implausible. The sign of this bias for the ATT_M=1 and CDE_M=1 can also be shown to be negative under Assumption 1–4, except in the implausible edge cases described in the Online Appendix. Thus, regardless of the target quantity, the use of the observed difference in means will understate the rate of racially discriminatory police violence. In addition, we emphasize that these derivations show that statistical bias remains even after assuming a “complete” set of control variables that renders race ignorable. Posttreatment conditioning induces bias unless additional assumptions hold.

POTENTIAL SOLUTIONS

How should the analyst proceed in light of these results? We propose two approaches that eliminate the highly implausible assumptions outlined in the “Strong Assumptions” section, which are unstated but implicit in prior work. We caution that these solutions still rely on the weaker assumptions described in the “Necessary Assumptions” section, although we argue that these are often plausible in light of insights from extensive research on policing. Reasonable people can disagree on the plausibility of various assumptions, but by stating them explicitly, we seek to advance empirical work in an area which, at present, largely ignores such issues altogether.

In the first approach, we derive nonparametric sharp bounds representing the tightest possible range of causal effects that are consistent with the reported data (Manski Reference Manski1995). Again, for simplicity, we begin by presenting bounds for the case in which treatment is unconditionally ignorable. To incorporate covariates, Online Appendix A.4 then describes a more general formulation in which bounds are computed within levels of X, without functional form assumptions, and reaggregated; this latter formulation is also applicable when a correctly specified regression is used. Both cases are demonstrated in a reanalysis of Fryer (Reference Fryer2019) below.

A key limitation of the first proposed solution is that all quantities of interest remain only partially identified. This is fundamentally a consequence of selection into police administrative records; point identification simply cannot be achieved without either implausible assumptions or additional data. To this end, we outline an alternative approach that incorporates limited information about the missing encounters (those that do not result in a stop). We show that with additional data—which in some cases are already being collected by agencies—the prevalence of racially discriminatory stops and most racial effects of interest can be point identified. Following our applied example, we describe a feasible research design based on this approach in detail.

Bounds on Effect of Race

Here, we derive large-sample nonparametric sharp bounds on the ATE_M=1 and ATT_M=1, focusing first on the case in which Assumption 4 (treatment ignorability) holds without conditioning on further covariates. Proposition 1 quantifies and corrects for the range of possible bias induced by posttreatment conditioning, producing an informative interval of possible joint values for (1) the partially identified ATE_M=1 and (2) the proportion of racial stops among reported minority encounters, ρ = Pr(M _i(0) = 0|D _i = 1, M _i = 1). As equation (6) suggests, when there is no racial bias in police stops (ρ = 0), these bounds collapse on the observed difference in means. We further demonstrate in Figure 4 that these bounds are highly informative when ρ is known or can be credibly estimated from supplemental data. When the prevalence of racially discriminatory detainment is unknown but a plausible range can be inferred from prior work, Figure 4 (discussed below) illustrates how this value can be used to assess the behavior of the bounds much like a sensitivity parameter.

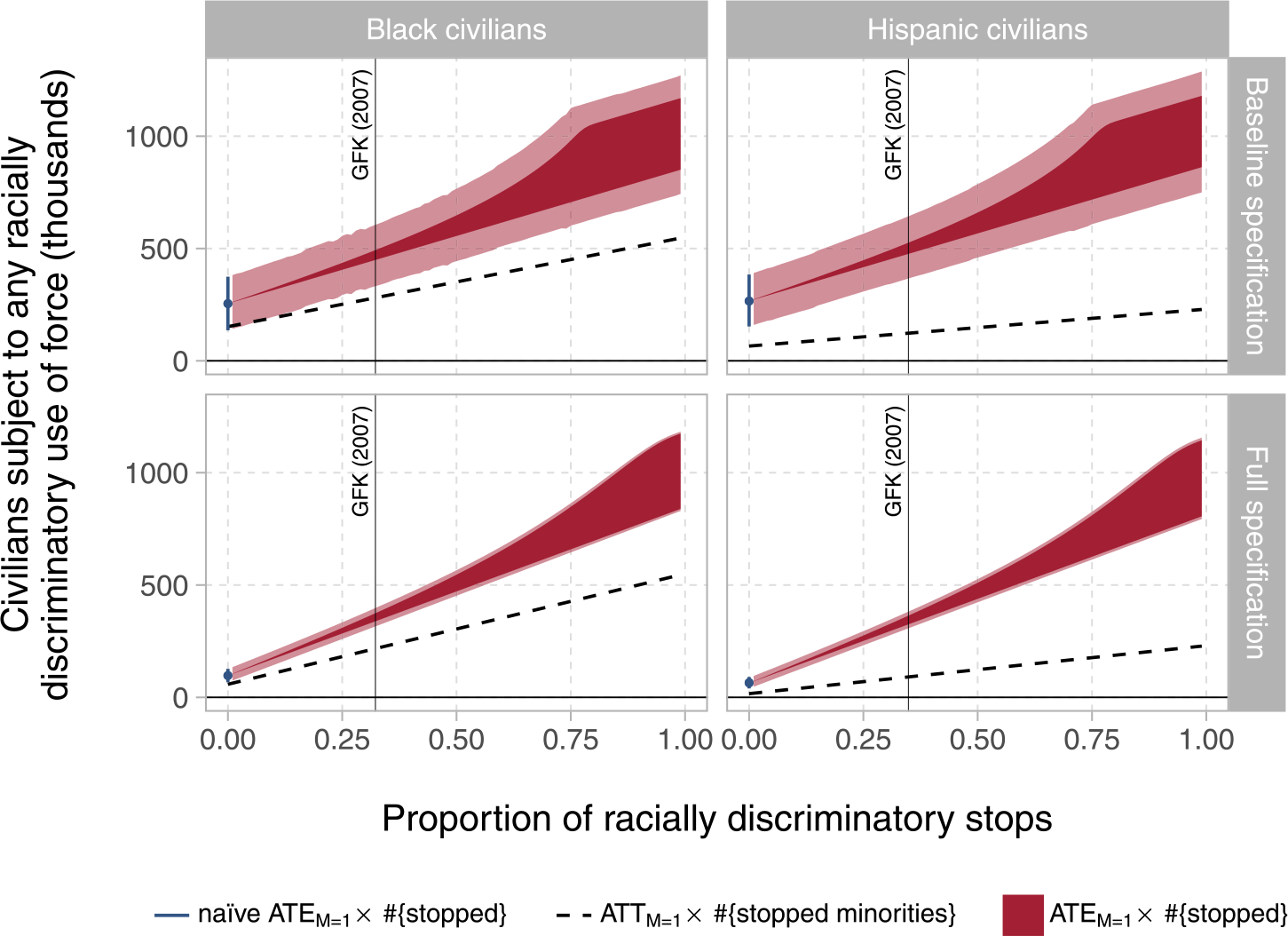
FIGURE 4. Bounds for Racially Discriminatory Use of Force, any Severity

Notes: These plots present the ATE_M=1 (ATT_M=1) for excess racial force, scaled by the number of stops (number of minority stops) to obtain the total number of civilians affected. The left panels consider the difference in the use of force if black civilians were substituted into each encounter of any race (each black encounter), versus white civilians; the right panels show the same quantities for Hispanic civilians. Blue points (error bars) denote the naïve estimator (95% confidence intervals), which, conditional on the typical selection-on-observables assumption, is unbiased for the ATE_M=1 if there are no discriminatory stops of minority civilians (zero on the x-axis). The dark (light) regions represent the range of possible values (95% CI) for (1) the ATE_M=1 and (2) the proportion of discriminatory stops in reported data jointly, per Proposition 1. The vertical line corresponds to an estimate of the proportion of discriminatory stops from Gelman, Fagan, and Kiss (Reference Gelman, Fagan and Kiss2007), suggesting a plausible value for this unobservable parameter. The top (bottom) panels present bounds based on a model with no controls (the main specification, adjusting for a wide range of covariates).

Proposition 1 (Nonparametric Sharp Bounds on ATE_M=1).When D _iis ignorable, nonparametric sharp bounds on (ATE _M=1, ρ) under Assumptions 1–4 are jointly given by

$$\eqalign{ {\mathbb{E}}\left[ {\hat{\Delta }} \right] + \rho {\mathbb{E}}\left[ {{Y_i}|{D_i} = 0,{M_i} = 1} \right]\left( {1 - \Pr \left( {{D_i} = 0|{M_i} = 1} \right)} \right) \,\,\,\,\,\le {\rm{AT}}{{\rm{E}}_{M = 1}} \le {\mathbb{E}}\left[ {\hat{\Delta }} \right] + {\rho \over {1 - \rho }}\left( {{\mathbb{E}}\left[ {{Y_i}|{D_i} = 1,{M_i} = 1} \right] - \max \left\{ {0,1 + {1 \over \rho }{\mathbb{E}}\left[ {{Y_i}|{D_i} = 1,{M_i} = 1} \right] - {1 \over \rho } \right} \bigg\}\right)\times\Pr \left( {{D_i} = 0|{M_i} = 1} \right) + \rho \,{\mathbb{E}}\left[ {{Y_i}|{D_i} = 0,{M_i} = 1} \right]\left( {1 - \Pr \left( {{D_i} = 0|{M_i} = 1} \right)} \right). \cr}$$

where $\hat{\Delta } = \overline {{Y_i}|{D_i} = 1,{M_i} = 1} - \overline {{Y_i}|{D_i} = 0,{M_i} = 1}$ and the (ATT _M=1, ρ) must similarly satisfy

$${\rm{AT}}{{\rm{T}}_{M = 1}} = {\mathbb{E}}\left[ {\hat{\Delta }} \right] + \rho {\mathbb{E}}\left[ {{Y_i}|{D_i} = 0,{M_i} = 1} \right]$$

To derive Proposition 1, we reformulate the bias in terms of the unobserved joint distribution of (1) the use of force in minority encounters and (2) whether a minority stop was racially discriminatory. Following Knox et al. (Reference Knox, Yamamoto, Baum and Berinsky2019), we then use Assumptions 1–4 and the Fréchet inequalities, in conjunction with the observed margins, to place sharp bounds on this joint distribution. These then imply sharp bounds on the ATE_M=1. A detailed proof is given in Online Appendix A.4 for the more general case in which D _i is ignorable only after conditioning on prestop covariates. In this case, the local average treatment effect, ATE_M=1,x, is first bounded by applying Proposition 1 within levels of X to obtain local bounds, $\left[ {{{\underline {{\rm{ATE}}} }_{M = 1,x}},{{\overline {{\rm{ATE}}} }_{M = 1,x}}} \right]$ . These are then straightforwardly reaggregated to obtain bounds on the conditional treatment effect among stops, $\left[ {\sum\limits_x {{{\underline {{\rm{ATE}}} }_{M = 1,x}}\Pr \left( {{X_i} = x|{M_i} = 1} \right)} } \right.$ , $\left. {\sum\limits_x {{{\overline {ATE} }_{M = 1,x}}\Pr \left( {{X_i} = x|{M_i} = 1} \right)} } \right]$ . In Online Appendix A1.5, we outline a Monte Carlo procedure for constructing confidence intervals that asymptotically contain both the true lower and upper bounds endpoints with probability 1 − α.

We note that the proportion of racially discriminatory stops may vary with X. However, when using these bounds as a sensitivity analysis, we suggest using the simplifying approximation of a constant ρ. This is because without additional data beyond civilian race, the use of force, or even prestop covariates, police administrative records alone are virtually uninformative about the range of ρ: any value in [0, 1) could produce the observed data,^{Footnote 10} although Proposition 1 shows that each possible ρ value has differing implications for the set of possible racial effects.

Point Identification of the ATE Given Additional Data

The ATE is point identified with the collection of only two additional numbers—the count of total minority and white encounters, within levels of X where applicable. Below, we propose an alternative design in which these data are collected from passive instruments such as traffic cameras or police body-worn cameras. Where such a design is infeasible (e.g., where traffic cameras cover only a subset of the jurisdiction under study), point identification can also be achieved by linking incomplete data on both reported and unreported encounters to police administrative records under mild assumptions.

Proposition 2 (Point Identification of ATE).Under Assumptions 1–4, the ATE is identified by a weighted combination of the observed racial means,

$${\hskip-55pt\mathbb{E}}\left[ {{Y_i}|{D_i} = 1,{M_i}\left( {{D_i}} \right) = 1} \right]\Pr \left( {{M_i} = 1|{D_i} = 1} \right) - {\mathbb{E}}\left[ {{Y_i}|{D_i} = 0,{M_i}\left( {{D_i}} \right) = 1} \right]\Pr \left( {{M_i} = 1|{D_i} = 0} \right).$$

Intuitively, the proof breaks the ATE into the size-weighted sum of principal effects among always-stop and racial-stop encounters (the principal effect in never-stop encounters is known to be zero). Crucially, the additional data on nonstops allows the researcher to construct a contingency table representing the joint distribution of race and detainment. As part of the proof in Online Appendix A.6, we show that this can be used to straightforwardly recover the size of each principal stratum under Assumptions 2 and 4(a). However, it remains impossible to determine whether any individual stop was racially discriminatory.

When total encounter numbers are unknown, this joint distribution can nonetheless be estimated by attempting to link a representative sample of all encounters (e.g., using timestamps from traffic cameras) against administrative records (e.g., license plate databases); those that are unlinkable can be presumed unreported. After recovering principal strata sizes, we then proceed by noting that minority outcomes in reported administrative data are in fact a mixture of Y _i(1, M _i(1)) from both always-stop and racial-stop strata in precisely the required proportions; that reported white outcomes correspond to Y _i(0, M _i(0)) from the always-stop stratum; and that Y _i(0, M _i(0)) is known to be zero among the racial-stop stratum under Assumption 1. From this, the ATE can then be reconstructed.

REANALYSIS OF FRYER (Reference Fryer2019)

We have shown that the standard approach to estimating racial bias in police data will always underestimate its degree, so long as police discriminate against minorities when choosing whom to investigate. To explore the magnitude of this statistical bias in an applied setting, we replicate and extend a section of Fryer (Reference Fryer2019) which reports estimates of racial discrimination in the application of sublethal force using the NYPD’s “Stop, Question and Frisk” (SQF) database (2003–13).^{Footnote 11} The NYPD data contain roughly 5 million records of pedestrian stops, the vast majority of which are of nonwhite suspects. The data record the use of varying levels of force, including laying hands on a suspect, handcuffing a suspect, pointing a weapon at a suspect, and pepper spraying a suspect, among others. The original analysis in Fryer (Reference Fryer2019) utilized the simple naïve approach of equation (1) to predict the severity of force applied by police, as well as covariate-adjusted naïve models analogous to those we consider in Appendices A.1–A.3. Specifically, the study presented a logistic regression of police force on suspect race, along with additional specifications that added a host of control variables such as precinct fixed effects, to render the ignorability assumptions more plausible. We reproduce two of these models—the baseline specification including only racial group indicators, along with the richer “main specification” (21)^{Footnote 12}—to estimate the conditional expectations in Proposition 1. For comparability to the original analysis, we take these models at face value, setting aside issues of potential model misspecification and the ignorability of civilian race.

One analysis in Fryer (Reference Fryer2019) considered the use of any force against a suspect, while subsequent analyses examined force exceeding various severity thresholds, such as a binary outcome for “at least use of handcuffs.” Using the coding rules and estimation procedures in Fryer (Reference Fryer2019), we were able to closely replicate the published results. However, in doing so, we discovered this procedure involved an unconventional and inadvisable step in which all observations with nonzero force below the threshold of interest were dropped—a severe case of selection on the dependent variable. In the most extreme case, in the analysis of police baton and pepper spray use, this resulted in the discarding of all encounters in which only lower levels of force were used, a set that comprised 21.5% of all observations and 99.8% of all uses of force. To present the most defensible results possible, for these outcomes, we depart from the analysis in Fryer (Reference Fryer2019) and revise the procedure so that all encounters with a level of force at or above a given threshold are assigned an outcome of 1 (as before) and all other encounters are assigned a value of 0 (including those with lower levels of force, which are now retained). Section B.1 in the Online Appendix contains an extended discussion of the issue; a comparison of the original, replicated, and corrected results; and a demonstration of the serious implications for statistical significance of the original estimates.

Based on the discussion in both Fryer (Reference Fryer2018) and Fryer (Reference Fryer2019), we interpret the published results as estimates of the ATE_M=1: “the difference in Y that can be attributed to an individual’s race,” (Fryer Reference Fryer2018, 2), conditional on a recorded interaction with police (i.e., conditional on M _i = 1). We note that of the other quantities considered in this study, the unconditional ATE cannot be estimated without information on unreported encounters, and the CDE_M=1 cannot be computed without strong assumptions about potential outcomes that can never be realized in observational settings. For these reasons, we focus on the ATE_M=1 and ATT_M=1 in this reanalysis.^{Footnote 13}

Figure 4 depicts bounds on the ATE_M=1 when the binary outcome is any use of force, including the lowest recorded value of physically handling a civilian.^{Footnote 14} Importantly, this specific outcome is unaffected by the outcome coding issue discussed above. (In Figures B.2 and B.3, we present additional bounds for varying force thresholds, up to whether a baton or pepper spray was used.) The plots also display estimates of the bias-corrected ATT_M=1 (dashed lines). As the plots show, the range of possible ATE_M=1 and ATT_M=1 values varies strongly with the severity of discrimination in stops.

In equation (6), we demonstrated that the use of the naïve estimator implied the substantively implausible assumption that police never discriminate in stops (i.e., ρ = 0). Similarly, contextual information also suggests that some depicted values of ρ are implausibly large. To understand the range of empirically plausible values, we turn to two prior studies that use very different analytic approaches to shed light on the degree of racial bias in the decision to detain civilians. Using the SQF data and controlling for precinct, suspected crime, and prior local arrest rates by race, Gelman, Fagan, and Kiss (Reference Gelman, Fagan and Kiss2007) produce estimates that—by our calculations—imply 32% of black-civilian stops made by the NYPD could not be explained even by differential criminality between racial groups of suspects, as proxied by prior arrest rates.^{Footnote 15} Their analyses are run separately by precinct and crime type; for simplicity, we take the weighted average of racial-stop proportions. This analytic approach most likely underestimates the proportion of racially discriminatory stops—the number of prior arrests in a precinct and racial group is not a direct measure of criminality, but is itself likely contaminated by discrimination in previous detainments and arrests. We, therefore, regard the value of ρ implied by Gelman, Fagan, and Kiss (Reference Gelman, Fagan and Kiss2007) as conservative.

Goel, Rao, and Shroff (Reference Goel, Rao and Shroff2016) take an entirely different tack based on a comparison of “hit rates,” or the share of stops that produced evidence of the suspected crime for which the civilian was detained—a variant of an “outcome test” for discrimination (Anwar and Fang Reference Anwar and Fang2006; Knowles, Perisco, and Todd Reference Knowles, Perisco and Todd2001). Using a flexible logistic regression to adjust for a vast array of indicators visible to officers prestop, the study shows that white hit rates exceeded those of “similarly situated” black civilians. We show in our Online Appendix A.7 that the difference in hit rates implies a minimum proportion of racial stops and, therefore, also implies a conservative estimate of ρ.^{Footnote 16} The corresponding values of ρ from these two studies are 0.32 and a lower bound of 0.34, respectively, when considering black civilians. While any estimate of this difficult-to-measure quantity from police data is sure to be imperfect, the fact that two independent estimates of racial bias in stopping so closely comport with one another, despite using wholly different analytical approaches, gives us some empirical justification for narrowing the range of plausible racial effects in the use-of-force analysis. We note that the research design presented in the “Recommendations for Future Research” section below offers an alternative approach for obtaining better estimates of racially discriminatory stopping.

Figure 4 demonstrates that strong negative bias in the naïve estimator paints a wildly misleading portrait of police use of force. We turn first to estimates of the ATE_M=1 using the main specification, which adjusts for a battery of covariates. The naïve estimator (which assumes no racial bias in police stops) suggests that encounters with black (Hispanic) suspects are predicted to exhibit an additional 3.9 (0.4) instances of handcuffing per 1,000 encounters, compared with the same encounters had they involved white civilians. We then employ the most conservative racial stopping estimate, denoted by the vertical line in the figure, to generate bounds on the true race effect. Our bias-corrected results show the true effect is at least as high as 15.5 (13.0)—meaning that the conventional approach underestimates discriminatory force by a factor of at least 4 (32).

To characterize bias in estimates of the ATT_M=1, we again use the conservative racial stopping estimate from Gelman, Fagan, and Kiss (Reference Gelman, Fagan and Kiss2007) to correct the naïve estimate. Again, the naïve approach substantially understates racially discriminatory police violence, suggesting that there were 75,000 instances in which police laid hands on black and Hispanic civilians, but would not have done so had those individuals been white. Our bias-corrected estimate shows the true number is approximately 307,000, meaning the naïve approach masks 232,000 such incidents. Similarly, the naïve approach indicates roughly 3,400 racially discriminatory instances in which officers pointed a weapon at a black or Hispanic civilian, whereas the bias-corrected ATT_M=1 shows the true number is almost five times as large.

To see how this statistical bias affects estimates for different levels of force, Table 1 presents naïve estimates alongside ATE_M=1 bounds for excess force per 1,000 black and Hispanic encounters across the full spectrum of police actions—ranging from physical handling of a civilian to the use of pepper spray or a baton—again using the conservative racial-stop estimate from Gelman, Fagan, and Kiss (Reference Gelman, Fagan and Kiss2007) to apply our bias correction. The results again show that the traditional approach substantially understates the degree of racial bias in police use of force. Our results also include numerous cases in which downward bias produces the illusion of no race effect. For example, while the approach in Fryer (Reference Fryer2019) implies a statistically insignificant 2.4 instances per 1,000 encounters of pushing Hispanic suspects to a wall due to suspect race, our revised estimate shows the true number is at least 26—eleven times larger. We can also quantify the number of masked instances of racially discriminatory uses of force as a percentage of all uses of force against minorities, displayed in Figure 5. In the period we examine, black and Hispanic civilians experienced force at the hands of police 779,894 times. Using the approach in Fryer (Reference Fryer2019), one would conclude that about 10% would not have occurred had those civilians been white. Using our bias-corrected approach, we find that in fact 39% were discriminatory. These underestimates persist across all force threshold analyses.^{Footnote 17}

TABLE 1. Average Treatment Effect among Stops (ATE_M=1), by Severity of Force and Minority Group

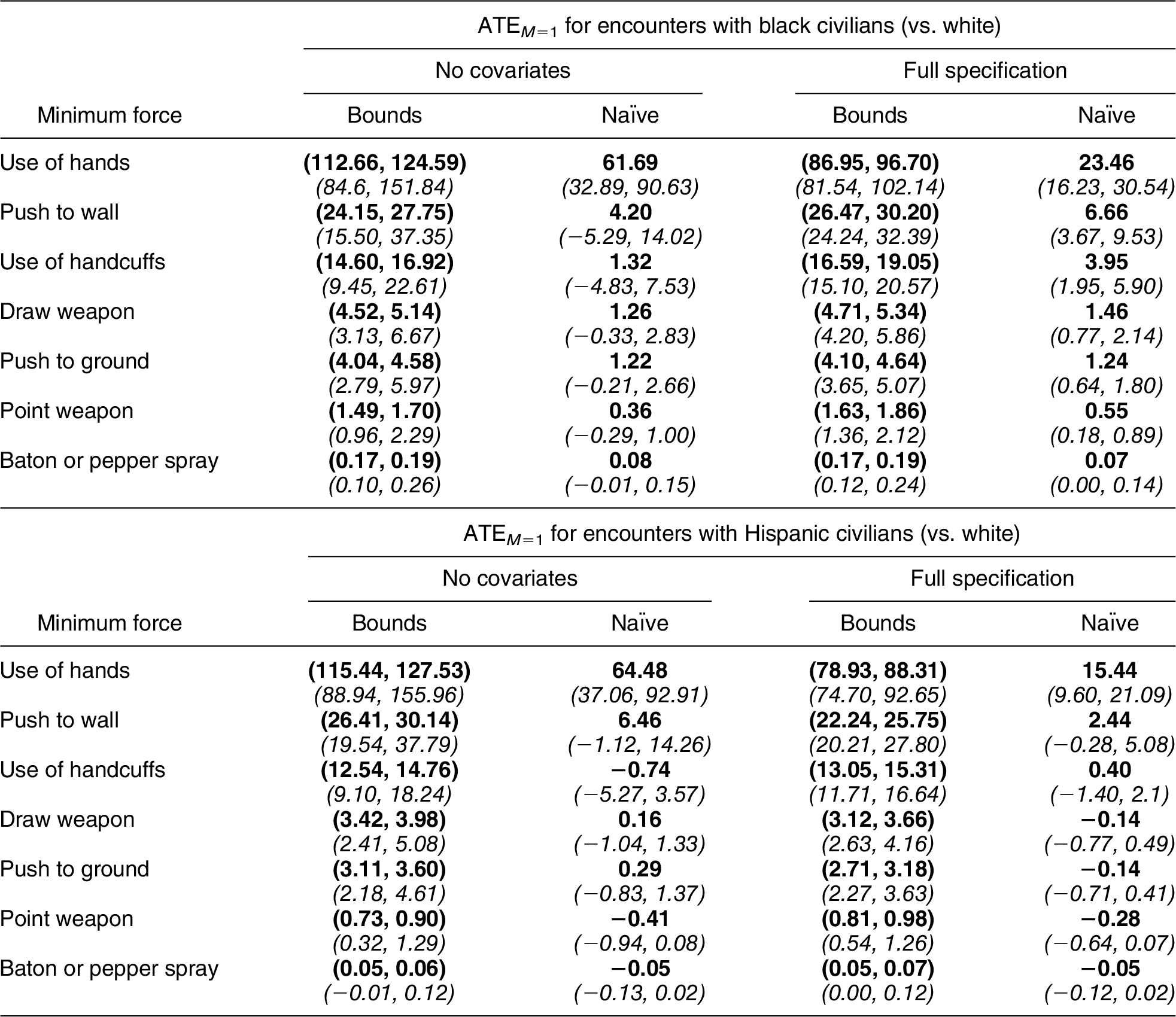
Note: Excess use of force used against minority civilians (versus white civilians) per 1,000 encounters. Bounds intervals indicate the range of possible ATE_M=1 values when the unknown proportion of discriminatory stops is approximated with the conservative estimate from Gelman, Fagan, and Kiss (Reference Gelman, Fagan and Kiss2007). Estimates are bolded, and 95% confidence intervals are italicized.

FIGURE 5. Estimated Number of Racially Discriminatory Uses of Force against Black and Hispanic Civilians, Divided by Total Observed Uses of Force among Those Groups Using Naïve (Red Dot) and Bias-Corrected (Blue Triangle) Estimators of the ATT _M=1

Notes: In some cases, the naïve approach returns negative estimates, indicating that more uses of force would have occurred had the civilians been white. The bias-corrected estimates show the naïve estimates substantially underestimate the pervasiveness of anti-minorityracial bias in police violence.

RECOMMENDATIONS FOR FUTURE RESEARCH

The analysis above clarifies whether and when estimates of racial bias in police behavior identify causal quantities, shedding light on how traditional estimation approaches that fail to account for posttreatment conditioning can inadvertently mask racially biased policing. Our results suggest the body of evidence on this topic that relies on police administrative data may be largely uninformative or even misleading. While our bias-correction and bounding techniques are an improvement, they still rely on assumptions that many analysts may not be willing to entertain. Some of these assumptions, such as conditional treatment ignorability, are unavoidable. But others can be sidestepped or weakened through the use of research designs that preempt the problem of posttreatment conditioning. In what follows, we detail a feasible research design that addresses these concerns.

To estimate the effect of suspect race on poststop police behavior while avoiding the concerns outlined above, we describe a feasible study of police–civilian interactions during traffic stops. A key advantage of traffic studies is that much of the data needed to improve research are already collected passively by law enforcement agencies across the United States in an automated fashion via highway cameras. We note that before the advent of this technology, data on unreported police–civilian interactions had to be manually collected by researchers accompanying patrol officers on their shifts (Allen Reference Allen1982; Smith, Visher, and Davidson Reference Smith, Visher and Davidson1984), a labor-intensive strategy highly vulnerable to researcher demand effects (Orne Reference Orne1962).

Recall that a key problem in the typical study of police administrative data is the unobservability of those encounters that do not generate police reports. However, given the prevalence of highway speed cameras across police jurisdictions, it is entirely feasible to collect data on every passing car (or a random sample of passing cars), whether or not police pulled the car over and recorded the stop. This mode of data collection has already been utilized in prior work (Kocieniewski Reference Kocieniewski2002; Lange, Johnson, and Voas Reference Lange, Johnson and Voas2005), though in those studies, camera data on individual motorists were not linked to administrative data on policing outcomes, as we propose below.

Given a large random sample of passing cars captured by highway speed cameras, analysts could use video or photographic records to document license plate numbers that allow for a merge with other administrative data sets containing information on the registrant’s home neighborhood, whether each car went on to be stopped by nearby police at a proximate time, whether a summons was issued, and whether the encounter escalated to include a search or the use of force. As with all causal analyses of observational data, analysts must still make some version of Assumption 4(b)—no treatment-outcome confounding conditional on observable covariates—but in this case, the standard “treatment selection on observables” plausibly holds because virtually all prestop data available to an officer are in fact observable to the analyst. Using camera footage merged with administrative records, analysts could credibly measure this “complete” set of control variables.^{Footnote 18} These factors would include not only the race, age, gender, and registered neighborhood of the driver but also the make, color, and condition of the car, along with weather and driving speed.

Given this set of covariates, researchers could credibly estimate the ATE for various outcomes, including searching, ticketing, and the use of force, by comparing the rates of outcomes between racial minority and majority motorists, regardless of whether they were stopped by police, conditional on X. The ATT_M=1 is similarly point identified because the proportion of racial stops can be calculated and used to correct estimates. However, the ATE_M=1 remains partially identified—the quantity can be bounded, as we show above, but not precisely estimated. And as Figure 6 makes clear, the CDE_M=1 remains fundamentally unidentifiable without covariates that make Assumption 5 plausible, such as controls for officer temperament that are specific to some stops but not others (i.e., time-varying), which likely influences both stopping decisions and subsequent treatment of civilians.

FIGURE 6. Traffic Stop Design

Notes: The DAG illustrates potential back-door paths for stops (through W, e.g., heavily policed neighborhoods) and for the use of force (through V, e.g., car registrant has warrant for arrest) that may correlate with the presence of minority drivers. These are blocked (boxed) by conditioning on prestop variables, including license plates as well as administrative records that can be linked through them. Many mediator-outcome confounders (U) cannot be blocked but do not pose a threat to inference for the ATE or ATE_M=1.

SUPPLEMENTARY MATERIAL

To view supplementary material for this article, please visit https://doi.org/10.1017/S0003055420000039.

Replication materials can be found on Dataverse at: https://doi.org/10.7910/DVN/KFQOCV.