More than petards or stilettoes, therefore, words—uncontrolled words, circulating freely, underground, rebelliously, not gotten up in dress uniforms, uncertified—frighten tyrants. But sometimes it is the official, uniformed, certified words that bring about the revolution.
– Ryszard Kapuściński, Shah of Shahs Footnote 1
Autocratic governments, despite their seemingly unconstrained authority, live in the shadow of mass political unrest. At any given moment, the public may reject the existing political order and—through action (strikes/protests) in the streets—impose substantial costs upon their leaders, sometimes even ousting the leadership or upending the regime. This is one of two threats that sitting autocrats must negotiate in their decision-making: Mass mobilization constitutes the threat from below.Footnote 2 Autocratic leaders must also be concerned with threats to the existing regime emerging from within their own ruling coalition.Footnote 3
Those who would participate in mass unrest against their political leadership face a critical problem: While protests or strikes that draw widespread participation are capable of forcing the hands of their rulers, protests that do not pass this threshold may be put down, often quite violently and at considerable cost to participants. The willingness of any one citizen to participate in antiregime mobilizations is therefore contingent on the willingness of others to similarly participate (Bueno de Mesquita Reference Bueno de Mesquita2010; Casper and Tyson Reference Casper and Tyson2014; Kuran Reference Kuran1991; Little Reference Little2012; Little, Tucker, and LaGatta Reference Little, Tucker and LaGatta2015; Lohmann Reference Lohmann1993; Shadmehr and Bernhardt Reference Shadmehr and Bernhardt2011). Participation in mobilization is subject to strategic complementarities—a given citizen grows more willing to engage in protest as she believes others are similarly willing to mobilize. But what then enables citizens to form shared beliefs in a manner that allows for protest?
In this article, we examine the role the informational environment plays in facilitating or inhibiting collective action, and how information translates into the stability of autocratic leaders.Footnote 4 In particular, we focus on the presence or absence of publicly observable information on governments’ economic performance. Publicly observable information plays an outsized role in interactions characterized by strategic complementarities, since such information allows citizens to not only update their beliefs about government performance, but also to update their higher order beliefs—their beliefs about the beliefs held by other citizens (Morris and Shin Reference Morris and Shin2002).Footnote 5 Publicly observable economic information thus facilitates the formation of shared expectations about the likely success of mass mobilization, rendering such mobilization feasible where absent such information it would be impossible.
We contend that, under autocratic rule, the availability of public economic information—which we term transparency—facilitates collective action and so renders regimes more vulnerable to threats from below.Footnote 6 This effect is most evident in economically under-performing regimes—when transparency reveals to the mass public that the leadership is underperforming and ensures that this perception is widely shared. However, for plausible parameter values in our model, transparency eases mobilization to a sufficient extent that the ruling regime is destabilized even without conditioning on the level of economic performance.
To anticipate our empirical results, we find support for our main theoretical predictions: transparency is associated with an increased risk of autocrat removal via mass revolt or democratization. These findings are associational—they do not demonstrate that transparency causes increased protests under autocracy. Given the relative infrequency of such events and the cross-national nature of these data, proof of causality is extraordinarily difficult. However, we do conduct a number of additional analyses, which serve to strengthen our contention that the mechanisms we describe are at work.
We demonstrate the following: (1) Transparency is associated with an increased risk of regime removal via mass unrest or via a transition to democracy. It is not, however, associated with other forms of autocratic instability. Notably, transparency is associated with a reduced risk of a coup. (2) Transparency is associated with more frequent protests and strikes. It is not, however, associated with other forms of unrest such as assassinations or guerrilla movements. Finally, we note that elsewhere (Hollyer, Rosendorff, and Vreeland Reference Hollyer, Rosendorff and Vreeland2015a), we demonstrate that transparency is associated with democratic stability.
Transparency, therefore, does not merely proxy for an unmeasured source of government weakness. Transparency is associated with the stability of democratic regimes, implying that any alternative mechanism must have the opposite effect in autocracies and democracies. Finally, while autocratic leaders may adopt transparency in an attempt to assuage public dissatisfaction through (partial) liberalization, it does not appear that these attempts are successful—increased levels of transparency are associated with more frequent strikes and antigovernment demonstrations.Footnote 7 Our findings on transparency thus stand in contrast to the effects of other forms of liberalization—such as opening to the formation of opposition parties or the conduct of autocratic elections—where the opposition may be successfully co-oped or cowed into supporting the regime (Blaydes Reference Blaydes2011; Brancati Reference Brancati2014; Gandhi Reference Gandhi2008; Little, Tucker, and LaGatta Reference Little, Tucker and LaGatta2015; Lust-Okar Reference Lust-Okar2006; Schedler Reference Schedler2002). Transparency instead plays a destabilizing role, similar to traditional accounts of the effect of liberalization under autocratic rule (Huntington Reference Huntington1968).Footnote 8
This set of results cannot fully insulate our findings from the threat of endogeneity. Indeed, we acknowledge that endogeneity persists—our estimates are likely to be biased. These tests do, however, suggest that such biases are unlikely to be large and that plausible alternative explanations for any one result cannot systematically explain all our empirical findings.
In what follows, we first outline our argument in greater detail. We then formalize these intuitions using a game theoretic model of collective action and transparency. This model predicts (1) that—for a broad range of parameter values—transparency is associated with a greater risk to autocratic survival, (2) that transparency increases instability more in low-growth environments, and (3) that transparency is specifically associated with mass mobilization (strikes, demonstrations). We then empirically test all three implications, using a measure of transparency that reflects the reporting/nonreporting of economic data to the World Bank. To foreshadow our results, we find significant evidence supporting claims (1) and (3). We find weaker support for claim (2). We additionally find no evidence that transparency increases other forms of unrest, such as assassinations, coups, or guerrilla movements. We conclude that this new measure of transparency has surprising effects on autocratic stability, as evidenced from a statistical analysis of claims advanced by an original theory.
ARGUMENT
Transparency and Unrest
The literature on autocratic regimes has emphasized the threat mass mobilization poses for regime stability. This is particularly true of the literature on democratization, which—insofar as democratization entails regime removal—is a form of instability (e.g., Acemoglu and Robinson Reference Acemoglu and Robinson2006; Boix Reference Boix2003; Przeworski Reference Przeworski2009; Rosendorff Reference Rosendorff2001). The threat that mass mobilization poses for autocratic leaders and ruling cliques—and the importance of attempts to repress or co-opt the masses—has played a prominent role in writings on authoritarian regimes more generally (e.g., Gandhi Reference Gandhi2008; Svolik Reference Svolik2012; Wintrobe Reference Wintrobe1998).
If mass unrest plays such a critical role in autocratic stability, what factors make unrest more or less likely? We address one such factor—government transparency—in this article.
Our conception of mass unrest begins with the observation—attributable to Kuran (Reference Kuran1991) and Lohmann (Reference Lohmann1993)—that protest is subject to a collective action problem. The costs (or benefits) any citizen faces from engaging in protest are falling (rising) in the number of her fellow citizens who similarly choose to protest—mass unrest is subject to strategic complementarities. These complementarities may arise from the logistics of repression—for a given level of government response, the probability that a particular protester is arrested or physically harmed falls as the number of her fellow protesters rises. Or, the odds of unseating or forcing compromises from the leadership rise with turnout.
The willingness of any given citizen to turn out in the streets is therefore dependent on her beliefs about whether her fellow citizens will similarly mobilize. In such an environment, publicly observable information will play an important role in citizen behavior. We focus on the role of publicly observable information regarding the economic performance of the sitting government. We contend that citizens are more likely to mobilize when they perceive that the ruling clique is mismanaging the economy, either as a result of its attempts to extract rents or simply as the result of incompetence (Haggard and Kaufman Reference Haggard and Kaufman1995; Przeworski et al. Reference Przeworski, Alvarez, Cheibub and Limongi2000).
Publicly available information plays a crucial role as it can (1) confirm or refute citizen perceptions of economic mismanagement and, critically, (2) it can also inform citizens about others’ beliefs regarding the extent of mismanagement. Each individual is aware that public information is also available to her fellow citizens, thus such information allows her to better judge others’ perceptions of the ruling elite. As citizens become more aware of one another’s perceptions, they become better able to judge the willingness of others to mobilize in protest.
The incentives to engage in unrest aimed at unseating the leadership are highest when the sitting regime has revealed itself to be either predacious or incompetent—i.e., when its economic performance is poor.Footnote 9 As greater amounts of public information on economic performance are made available, citizens are better able to assess the performance of the government. Citizen perceptions align more closely with economic reality. Each citizen is aware these beliefs are shared. Consequently, as transparency rises, the economic performance of the sitting government will translate more readily into manifestations of popular unrest. Transparency conditions the relationship between economic outcomes and unrest—making this correlation stronger.
If successfully unseating the sitting government via mass unrest is sufficiently “difficult”—i.e., if the costs to unrest are sufficiently large relative to the benefits of success, or the threshold of participation necessary to unseat the incumbent is sufficiently high—citizens will only engage in protest when highly certain of the government’s underperformance. Moreover, they must be similarly certain that this perception is widely shared. Without public disclosure of economic information, this level of certainty is unlikely to be attained. As the level of transparency rises, the threshold level of certainty necessary to facilitate unrest is more likely to be attained. Consequently, the unconditional probability of unrest rises with transparency.
Defining Transparency
The definition of transparency used here pertains to the collection and disclosure of credible economic data. Such data must be publicly disclosed—and known to be publicly disclosed—if citizens are to update their beliefs not only about government performance, but also their higher order beliefs about the perceptions of their fellow citizens. These data must be credible if citizens are to update their beliefs about government actions based upon the disclosed information. And they must be aggregated such that the experiences of a broad swath of the population are reflected in the numbers that are presented.
We draw our empirical measure of transparency from the HRV Index (Hollyer, Rosendorff, and Vreeland Reference Hollyer, Rosendorff and Vreeland2014)—a measure of data disclosure that captures these three aspects of our theoretical notion of transparency. This index is based upon the reporting/nonreporting of data to the World Bank’s World Development Indicators (WDI) data series (World Bank, N.d.). It summarizes the reporting of 240 variables selected from across the WDI. The reporting of these variables is summarized on a single dimension, through the use of an item response model—where transparency is treated as the latent tendency to report data. The result is a continuous transparency measure, that covers 125 countries from 1980 to 2010.
Because the WDI contains aggregate economic data which are collected by national statistical agencies and provided to international organizations, it constitutes a direct measure of the collection and dissemination of aggregate economic data. The disclosure of such data to the World Bank proxies for public disclosure more generally. Finally, these data are credible insofar as they survive the scrutiny of the World Bank’s review. Observations that are deemed “questionable” are deleted from the WDI.Footnote 10
Hollyer, Rosendorff and Vreeland (Reference Hollyer, Rosendorff and Vreeland2014) provide an extensive discussion of this index, and provide evidence of its validity. The HRV measure discriminates well among countries at all levels of transparency, it most strongly reflects the reporting of politically relevant data, and country case studies demonstrate that the index varies as expected with major political events (including episodes of well-known misreporting of data, for instance in Argentina). Disclosure, and hence HRV index scores, reflects both states’ willingness and capacity to disclose information to the general public. Both are necessary, but neither is sufficient, to ensure disclosure. Scores on this index are thus correlated with measures of state capacity, such as income per capita—though this correlation takes on a particular form. Hollyer, Rosendorff, and Vreeland (Reference Hollyer, Rosendorff and Vreeland2014) report that all incapable states, regardless of regime type, disclose at similar rates, whereas, among capable states, scores vary substantially between regime types with democracies reporting at higher rates than autocracies.
In a separate work, Hollyer, Rosendorff, and Vreeland (Reference Hollyer, Rosendorff and Vreeland2013) demonstrate that the HRV index is associated with other forms of transparency. The correlation between the HRV index and Freedom House’s Freedom of the Press measure is 0.62, the correlation between the HRV index and the World Bank’s newspaper circulation per capita measure is 0.59, and the correlation between the HRV index and the enactment of Freedom of Information Laws (FOILs) is 0.60. (By way of comparison, the correlation of the Freedom House measure with the other two measures is, respectively, 0.57 and 0.55.) Hollyer, Rosendorff, and Vreeland (Reference Hollyer, Rosendorff and Vreeland2013) further regress the HRV index against these alternative conceptions of transparency, a measure of democracy, and GDP per capita. In all such regressions, democracy remains a significant predictor of the HRV index, even after controlling for alternative measures of transparency and GDP per capita, whereas GDP per capita is never a significant predictor when the other controls are added. These results suggest that the HRV index is a political measure.
Nonetheless, in all regressions, we control for GDP per capita to help adjust for the correlation between disclosure and state capacity. Moreover, we note that any failure to fully control for capacity should bias against our findings, ceteris paribus we would expect capable autocratic regimes to be less prone to collapse.
Both the notion and measure of transparency that we employ here are thus narrowly defined. We conceive of transparency simply as the disclosure of data, not as a general conception of “openness,” which may pertain to any aspect of information transmission in a given polity. Alternative—often broader—conceptions of transparency have been employed elsewhere (Adserà, Boix, and Payne Reference Adserà, Boix and Payne2003; Berliner Reference Berliner2014; Besley and Burgess Reference Besley and Burgess2002; Broz Reference Broz2002; Dahl Reference Dahl1971; Djankov et al. Reference Djankov, McLiesh, Nenova and Shleifer2003; Grief Reference Grief2006; Habyarimana et al. Reference Habyarimana, Humphreys, Posner and Weinstein2009; Islam Reference Islam2006). We prefer our measure in this instance because it neatly conforms to the notion of transparency developed in our theoretical model.
Contrast with Democracies
Elsewhere (Hollyer, Rosendorff, and Vreeland Reference Hollyer, Rosendorff and Vreeland2015a), we examine the relationship between transparency and mass unrest in democratic regimes. Under democratic rule, our results are turned on their head. Transparency serves to insulate democratic regimes from mass unrest, even as it destabilizes autocracies.
The model we develop in Hollyer, Rosendorff, and Vreeland (Reference Hollyer, Rosendorff and Vreeland2015a) is similar to that we present below, with the addition of meaningful elections. In that model, transparency enhances the effectiveness of elections in addressing adverse selection problems in government. Voters are more likely to remove underperforming leaders via the ballot box, and retain those that perform well, as transparency rises. Since elections and unrest serve as substitute mechanisms through which the public may discipline its leaders, the incentive to resort to unrest falls as transparency rises.
Critically, autocracies differ from democracies because of the informational value of elections. As Fearon (Reference Fearon2011) notes, the electoral process serves to directly inform citizens of the distribution of discontent with the sitting leadership (see also, Hyde and Marinov Reference Hyde and Marinov2014; Little, Tucker, and LaGatta Reference Little, Tucker and LaGatta2015). Thus, regardless of the level of transparency, citizens in democracies have a great deal of information about the willingness of their fellows to engage in protest against their leadership.
By contrast, in autocracies, elections are either absent or sufficiently heavily manipulated to be uninformative of the distribution of discontent.Footnote 11
EXISTING LITERATURE
Our article thus most clearly relates to the literature on protests and mass mobilization—starting with Kuran’s (Reference Kuran1991) observation of the collective action problems involved in mass mobilization. Lohmann (Reference Lohmann1993) explicitly deals with the importance of information in such interactions, and with the role of costly signaling in solving collective action problems.
A more recent literature on mass protest and collective action similarly emphasizes the informational problems involved in coordinating protests (Shadmehr and Bernhardt Reference Shadmehr and Bernhardt2011). Many of these pieces stress the importance of mechanisms for disseminating information, hence easing the coordination of protest. For instance, revolutionary vanguards may serve to inform the broader public about the extent of discontent with the regime (Bueno de Mesquita Reference Bueno de Mesquita2010; Shadmehr and Bernhardt Reference Shadmehr and Bernhardt2013). Authoritarian elections may serve a similar purpose (Egorov and Sonin Reference Egorov and Sonin2012; Little, Tucker, and LaGatta Reference Little, Tucker and LaGatta2015). Protests may serve to resolve informational problems among the elite, facilitating coups (Casper and Tyson Reference Casper and Tyson2014). Edmond (Reference Edmond2013), Hollyer, Rosendorff, and Vreeland (Reference Hollyer, Rosendorff and Vreeland2015b), Lorentzen (Reference Lorentzen2014), and Shadmehr and Bernhardt (Reference Shadmehr and Bernhardt2015) all consider environments in which elites manipulate or censor information in the shadow of the threat of unrest.
Like these more recent works, our theoretical treatment of transparency and mass unrest builds on the mechanics of global games (Carlsson and van Damme Reference Carlsson and van Damme1993; Morris and Shin Reference Morris and Shin1998, Reference Morris and Shin2001). Our depiction of the role of transparency owes particularly to Morris and Shin (Reference Morris and Shin2002), who emphasize that—in the presence of strategic complementarities—public information plays a dual role, causing observers to update their own beliefs as well as their higher order beliefs about the beliefs of other players.
Our approach differs from existing treatments of protest in that we explicitly focus on the role of publicly available economic information. We do so in a model that is isomorphic to standard accounts of “retrospective” voting. This approach allows us to extend our model to democracies (see Hollyer, Rosendorff, and Vreeland Reference Hollyer, Rosendorff and Vreeland2015a), allowing us to capture institutional variation in a way as yet absent from the literature. This is, to our knowledge, also the first article in this literature to attempt to empirically test the predictions regarding the informational environment and protest.
We depart from global games literature in a technical assumption: Classical formulations of global games exhibit the property of two-sided limit dominance (Morris and Shin Reference Morris and Shin2001). For some realizations of their private signal, citizens have a dominant strategy: protest or not protest. By contrast, we treat protest as a “pure” coordination game, incorporating problems of incomplete information and a global games informational structure. Hence, unlike in classical global games, multiple equilibria always exist. Moreover, we assume away issues of free-riding in protest, in order to focus on problems of coordination. In making this assumption, however, our model is more directly comparable to treatments of political accountability in environments of incomplete information (Banks and Sundaram Reference Banks, Sundaram, Barnett, Schofield and Hinich1993; Besley Reference Besley2006; Fearon Reference Fearon, Przeworski, Stokes and Manin1999). In adopting this “pure” coordination game approach, we further dispense with the assumption, common in this literature, that some citizens have a dominant strategy of protesting—i.e., that these citizens would engage in protest even knowing that no others would join them on the streets (for another exception, see Bueno de Mesquita Reference Bueno de Mesquita2010).
Our findings also speak to an expansive literature on mass unrest and autocratic stability. Models of autocratic rule (Gandhi Reference Gandhi2008; Svolik Reference Svolik2012; Wintrobe, Reference Wintrobe1998) often assume that leaders are constrained by the threat of mass unrest, and must employ co-optation or repression to deal with this threat. Our results suggest when such pressures may be more or less acute. The literature on the stability of political regimes also often assumes the importance of mass threats from the populace. This is most obvious in models of democratization, wherein revolutionary activities on the part of the citizenry—or the threat thereof—may give rise either to the direct usurpation of authoritarian regimes or the extension of suffrage (Acemoglu and Robinson Reference Acemoglu and Robinson2006; Boix Reference Boix2003; Przeworski Reference Przeworski2009; Rosendorff Reference Rosendorff2001).Footnote 12 While our results speak to broader forms of autocratic instability than democratization, our findings are suggestive as to when this revolutionary threat may be more or less powerful.Footnote 13
Finally, we note that our article closely relates to an account of autocratic stability and transparency within autocratic regimes put forth by Boix and Svolik (Reference Boix and Svolik2013).Footnote 14 Like us, Boix and Svolik examine collective action problems in unseating autocratic leaders, and the role the informational environment plays in shaping these interactions. Unlike our article, however, Boix and Svolik concentrate on the threat of coups. Boix and Svolik’s conception of transparency differs radically from ours—in their article, transparency consists of clear rules of behavior, the violation of which may mobilize a coup. They conclude that this form of transparency reduces the frequency of coups. We, by contrast, focus on transparency as the public disclosure of economic information, and on the role this disclosure plays in coordinating mass unrest by the populace.Footnote 15
MODEL
Primitives
Consider an interaction between an autocratic leader L and a mass of citizens. Each citizen is denoted i where i is indexed over the unit interval i ∈ [0, 1].
Our model is one of adverse selection in government. Citizens seek to infer the leader’s type (θ ∈ {0, 1}), which may be either “good” (θ = 1) or “bad” (θ = 0). A leader’s type may refer to his level of skill, competence, or honesty. Good leaders will therefore return better economic performance than bad leaders. Citizens may seek to remove bad leaders from office, while retaining good types.
Nature chooses L’s type where θ = 1 with probability p and θ = 0 with probability 1 − p. In each period during which she is in office, L chooses whether to provide a public good Gt ∈ {0, 1}, where t ∈ {1, 2} denotes the period of play. L’s utility from doing so is a function of her type, such that in each periodFootnote 16
 $$\begin{eqnarray*}
u_{L,t}(G_t;\theta ) = \left\lbrace \begin{array}{l@{\hspace*{9pt}}l}1&\text{if}\, G_t=\theta ,\\
0&\text{otherwise,}\end{array}\right. \\
u_L &=&\sum _{t=1}^2 u_{L,t}(G_t,\theta ).
\end{eqnarray*}$$
$$\begin{eqnarray*}
u_{L,t}(G_t;\theta ) = \left\lbrace \begin{array}{l@{\hspace*{9pt}}l}1&\text{if}\, G_t=\theta ,\\
0&\text{otherwise,}\end{array}\right. \\
u_L &=&\sum _{t=1}^2 u_{L,t}(G_t,\theta ).
\end{eqnarray*}$$
L’s choice regarding public goods provision Gt
∈ {0, 1} has implications for economic outcomes in the following manner: Each citizen i receives an income y
i, t
= Gtg + ε
i, t
, where
![]() $\epsilon _{i,t} {}_{\widetilde{\scriptstyle {\rm iid}}} N(0,\sigma ^2_y)\, \forall \, i,t$
, and g is a strictly positive constant. The standard deviation of individual outcomes, σ
y
> 0, captures all factors exogenous to government policies that may shift a given citizen’s economic welfare. Each citizen observes y
i, t
, but does not observe the value of Gt
. In observing first period income, y
i, 1, the citizen is also receiving a signal about the type of government she is facing, which informs her decision about whether to engage in protest.
$\epsilon _{i,t} {}_{\widetilde{\scriptstyle {\rm iid}}} N(0,\sigma ^2_y)\, \forall \, i,t$
, and g is a strictly positive constant. The standard deviation of individual outcomes, σ
y
> 0, captures all factors exogenous to government policies that may shift a given citizen’s economic welfare. Each citizen observes y
i, t
, but does not observe the value of Gt
. In observing first period income, y
i, 1, the citizen is also receiving a signal about the type of government she is facing, which informs her decision about whether to engage in protest.
In the first period of play, all citizens also receive a publicly observable signal of the state of the economy s. We assume that s = G 1 g + ρ, where ρ ~ N(0, σ2 s ) and E[ρε i, t ] = 0 ∀ i, t, where σ s > 0 is the standard deviation of this publicly observed signal. s is meant to depict the role of publicly disclosed aggregate economic data, which enable citizens to form beliefs about government performance. As more information is made available, citizens are better able to discern the role of government policies in shaping economic outcomes—consequently σ s shrinks.Footnote 17 σ s is thus a measure of the inverse of transparency (i.e., of opacity). Since s depicts the public disclosure of aggregate economic data, we further assume that σ s < σ y .
Transparency, here, is an exogenous parameter of the model. We focus on the role transparency plays in fostering mobilization rather than the determinants of transparency. Elsewhere (Hollyer, Rosendorff, and Vreeland Reference Hollyer, Rosendorff and Vreeland2015b), we examine the incentives for autocrats to disclose, taking the results here on the relationship between transparency and mass mobilization as a theoretical prior. In that work, we demonstrate that transparency may insulate autocratic leaders from opposition that emerges from within the regime, in part because the increased mobilizational capacity of the populace renders attempts to discipline the leader more risky for members of the autocratic elite. The primary determinant of transparency is thus institutional—the ease with which members of the elite may sanction the leader—and varies little over time.Footnote 18
After receiving her signals (both public and private) of government performance, each citizen i may mobilize in an attempt to overthrow the sitting government, ai ∈ {0, 1}. Let the total number of citizens engaged in collective action be A ≡ ∫1 0 aidi. If A exceeds some exogenous threshold T ∈ (0, 1), the sitting government will be removed and replaced by a new L, whose type is drawn with the same distribution as the prior leader. We define an indicator function R(A) to denote removal, such that
Engaging in mobilization entails a cost of κ > 0 for each citizen. However, if the protest is successful in removing the sitting leader, each citizen who participates in these protests gains a benefit β > κ. These benefits may be thought of as the psychological returns from participating in the successful overthrow of the ancien regime, or as material benefits flowing from the likely favors from any new regime that replaces the old. In either case, β represents a form of “selective incentive” for mobilization (Olson Reference Olson1971). Each citizen’s utility function is
The order of play proceeds as follows:
-
1. Nature chooses L’s type θ ∈ {0, 1}. The value of θ is revealed to L, but not to any citizen.
-
2. L chooses whether to provide the public good G 1 ∈ {0, 1}.
-
3. Nature chooses ε i, 1 ∀ i and ρ. y i, 1 is revealed to each citizen i, but not to any other citizen. s is revealed to all citizens.
-
4. Each citizen chooses whether to engage in collective action ai ∈ {0, 1}.
-
5. If R(A) = 1, L is replaced and Nature draws the type of her replacement θ ∈ {0, 1}, where Pr(θ = 1) = p.
-
6. The sitting L chooses the value of G 2 ∈ {0, 1}.
-
7. Nature chooses ε i, 2 ∀ i. y i, 2 is realized for all citizens and the game ends.
Equilibrium
While this resembles a global games approach to mass unrest (Angeletos, Hellwig, and Pavan Reference Angeletos, Hellwig and Pavan2007; Casper and Tyson Reference Casper and Tyson2014) the game presented here does not satisfy the two-sided “limit dominance” condition (Morris and Shin Reference Morris and Shin1998)—there is no type of government for which political action is a dominant strategy for any signal. Consequently, multiple equilibria exist. In particular, two equilibria exist: one in which all citizens always mobilize, the other in which no citizen ever mobilizes. In the former instance, given the strategies of all other players, each i prefers to set ai = 1, and thus obtain the benefits β − κ > 0 of participating in the successful mobilization—regardless of her beliefs about the government’s type. Similarly, in the latter, given the strategies of all other citizens, each i prefers to set ai = 0—and thus avoid the cost κ > 0 of participating in an inevitably failed mobilization, regardless of her beliefs. We do not focus on these “all-in/all-out” equilibria because they require all citizens to believe, with certainty, that their countrymen will all either engage or not engage in political mobilization, and to believe that this will be the case regardless of the performance of the incumbent government. These equilibria strike us as unrealistic. Moreover, they are dominated on welfare grounds by an alternative equilibrium.
We instead focus on a pure strategy perfect Bayesian equilibrium (PBE) in which each citizen i conditions her mobilization strategy on both her signals y
i, 1 and s. We restrict attention to monotone equilibria in which higher signals are interpreted weakly as corresponding to an increased likelihood of a high type leader, and furthermore restrict attention to equilibria in which each i employs a cut-point strategy: i sets ai
= 1 if and only if y
i, 1 is less than some threshold value
![]() $\bar{y}$
(Bueno de Mesquita Reference Bueno de Mesquita2010). This threshold value
$\bar{y}$
(Bueno de Mesquita Reference Bueno de Mesquita2010). This threshold value
![]() $\bar{y}$
will be a function of the publicly observable signal (denoted
$\bar{y}$
will be a function of the publicly observable signal (denoted
![]() $\bar{y}(s)$
).
$\bar{y}(s)$
).
An equilibrium involving cut-point strategies has several desirable properties relative to the two all-in/all-out equilibria. The cut-point equilibrium involves citizens acting upon all available information, and the cut-point equilibrium probabilities of mass mobilization and of regime survival are conditional upon economic performance, which would not be true in the all-in/all-out equilibria. Finally, as we demonstrate in the Online Appendix, the cut-point equilibrium dominates the all-in/all-out equilibria on welfare considerations. If we define efficiency in the form of expected economic utility (setting aside the selective mobilization incentives and costs β, κ), citizens strictly prefer the cut-point equilibrium to the all-in/all-out equilibria.
A PBE requires that beliefs of the citizens be consistent with the strategy profile and Bayes’ rule, and that the strategy of any citizen and the leader be sequentially optimal given all the beliefs and the strategies of the other citizens (Fudenberg and Tirole Reference Fudenberg and Tirole1991). A cut-point PBE in monotone strategies is characterized by the following: (1) A threshold
![]() $\bar{y}(s): \mathbb {R} \rightarrow \mathbb {R} \cup \lbrace -\infty ,\infty \rbrace$
, where political action occurs whenever
$\bar{y}(s): \mathbb {R} \rightarrow \mathbb {R} \cup \lbrace -\infty ,\infty \rbrace$
, where political action occurs whenever
![]() $y_{i,1} < \bar{y}(s)$
for all i. Where
$y_{i,1} < \bar{y}(s)$
for all i. Where
![]() $\bar{y}(s)=-\infty$
, no citizen will ever mobilize; where
$\bar{y}(s)=-\infty$
, no citizen will ever mobilize; where
![]() $\bar{y}(s)=\infty$
, all citizens mobilize. (2) A strategy for L from type- to action-space, Gt
: {0, 1} → {0, 1}. (3) Posterior beliefs Pr(θ = 0|y
i, 1, s). We characterize each of these in turn; but first some preliminary definitions are necessary.
$\bar{y}(s)=\infty$
, all citizens mobilize. (2) A strategy for L from type- to action-space, Gt
: {0, 1} → {0, 1}. (3) Posterior beliefs Pr(θ = 0|y
i, 1, s). We characterize each of these in turn; but first some preliminary definitions are necessary.
Definition 1 Define
![]() $\bar{y}^*(s)$
implicitly by the value of y
i, 1 that solves
$\bar{y}^*(s)$
implicitly by the value of y
i, 1 that solves
This is the value of the private signal, given a public signal, that would yield posterior beliefs about the type of the leader such that the citizen is indifferent between taking political action and not, given that all the other citizens are behaving the same way. In the Online Appendix, we show that this is well defined. Using the definition of
![]() $\bar{y}^*(s)$
we can now specify
$\bar{y}^*(s)$
we can now specify
![]() $\bar{y}(s)$
as follows (where Φ is the CDF of the standard normal):
$\bar{y}(s)$
as follows (where Φ is the CDF of the standard normal):
Definition 2 Define
 $$\begin{eqnarray}
\bar{y}(s) = \left\lbrace \begin{array}{l@{\hspace*{9pt}}l}\infty &\text{if}\, \Phi (\frac{\bar{y}^*(s)-g}{\sigma _y})\ge T, \\
\bar{y}^*(s)&\text{if}\, \Phi (\frac{\bar{y}^*(s)}{\sigma _y}) \ge T > \Phi (\frac{\bar{y}^*(s)-g}{\sigma _y}), \\
-\infty &\text{if}\, \Phi (\frac{\bar{y}^*(s)}{\sigma _y}) < T.\end{array}\right.
\end{eqnarray}$$
$$\begin{eqnarray}
\bar{y}(s) = \left\lbrace \begin{array}{l@{\hspace*{9pt}}l}\infty &\text{if}\, \Phi (\frac{\bar{y}^*(s)-g}{\sigma _y})\ge T, \\
\bar{y}^*(s)&\text{if}\, \Phi (\frac{\bar{y}^*(s)}{\sigma _y}) \ge T > \Phi (\frac{\bar{y}^*(s)-g}{\sigma _y}), \\
-\infty &\text{if}\, \Phi (\frac{\bar{y}^*(s)}{\sigma _y}) < T.\end{array}\right.
\end{eqnarray}$$
The value of
![]() $\bar{y}(s)$
is the cut point that characterizes the equilibrium in which all citizens receiving a private signal below the cut point choose to engage in political action; those with signals higher than
$\bar{y}(s)$
is the cut point that characterizes the equilibrium in which all citizens receiving a private signal below the cut point choose to engage in political action; those with signals higher than
![]() $\bar{y}(s)$
stay off the streets. The equilibrium is simply stated as follows:
$\bar{y}(s)$
stay off the streets. The equilibrium is simply stated as follows:
Proposition 1 The following strategies and beliefs constitute a PBE.
-
1. Gt = θ for t = 1, 2.
-
2. ai = 1 if
 $y_{i,1} \le \bar{y}(s)$
and ai
= 0 otherwise, for all i.
$y_{i,1} \le \bar{y}(s)$
and ai
= 0 otherwise, for all i. -
3.
 $Pr(\theta =0|y_{i,1},s)=\frac{\phi (\frac{y_{i,1}}{\sigma _y})\phi (\frac{s}{\sigma _s})(1-p)}{p\phi (\frac{y_{i,1}-g}{\sigma _y})\phi (\frac{s-g}{\sigma _s}) + \phi (\frac{y_{i,1}}{\sigma _y})\phi (\frac{s}{\sigma _s})(1-p)}$
for all i (Bayes’ rule),
$Pr(\theta =0|y_{i,1},s)=\frac{\phi (\frac{y_{i,1}}{\sigma _y})\phi (\frac{s}{\sigma _s})(1-p)}{p\phi (\frac{y_{i,1}-g}{\sigma _y})\phi (\frac{s-g}{\sigma _s}) + \phi (\frac{y_{i,1}}{\sigma _y})\phi (\frac{s}{\sigma _s})(1-p)}$
for all i (Bayes’ rule),
where ϕ is the PDF of the standard normal.
All proofs are in the Online Appendix.
Intuitions
To develop the intuitions, consider first the leader’s decision. The leader always matches his action with his type—this is a dominant strategy. Good leaders maximize both their contemporaneous utility and the probability of retention by providing the public good. Bad types, on the other hand, receive a sufficiently high utility from withholding the public good today to more than offset any reduced probability of retention. Any citizen’s problem therefore is to try to refine her beliefs over the (hidden) action, and hence the type of the leader in office, based on both the private and public signals received.
If
![]() $\Phi (\frac{\bar{y}^*(s)}{\sigma _y}) \ge T > \Phi (\frac{\bar{y}^*(s)-g}{\sigma _y})$
, the critical mass of protesters needed to remove the incumbent leader is loosely speaking, “moderate.” Each citizen, after receiving both her private and public signals, computes her posterior beliefs about the type of leader she is facing, using Bayes’ rule. Along the equilibrium path, those citizens receiving a poor signal of the leader’s type engage in political action. Those receiving a high signal are inclined to believe that the government is of a high type, and would like to preserve the leader in office, and hence do not protest. Figure 1 demonstrates the individual decision made by any citizen.
$\Phi (\frac{\bar{y}^*(s)}{\sigma _y}) \ge T > \Phi (\frac{\bar{y}^*(s)-g}{\sigma _y})$
, the critical mass of protesters needed to remove the incumbent leader is loosely speaking, “moderate.” Each citizen, after receiving both her private and public signals, computes her posterior beliefs about the type of leader she is facing, using Bayes’ rule. Along the equilibrium path, those citizens receiving a poor signal of the leader’s type engage in political action. Those receiving a high signal are inclined to believe that the government is of a high type, and would like to preserve the leader in office, and hence do not protest. Figure 1 demonstrates the individual decision made by any citizen.
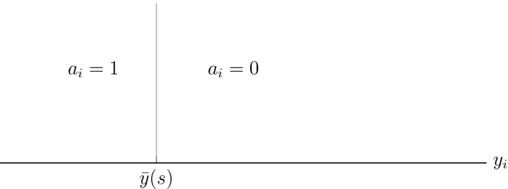
FIGURE 1. Individual Citizen’s Decision
Recall that there is a continuum of citizens. Therefore, given the equilibrium threshold, we can compute what fraction of the citizens will protest in equilibrium. This of course depends on the distribution of the private signals. If the leader is truly of type 0—the bad type—the distribution of signals received by the voters has mean zero. Then in Figure 2 we see that the fraction of the population that mobilizes when in fact θ = 0 is given by the light gray region, or more precisely,
![]() $\Phi (\scriptsize\frac{\bar{y}^*(s)}{\sigma _y} )$
, where Φ is the CDF of the standard normal.
$\Phi (\scriptsize\frac{\bar{y}^*(s)}{\sigma _y} )$
, where Φ is the CDF of the standard normal.
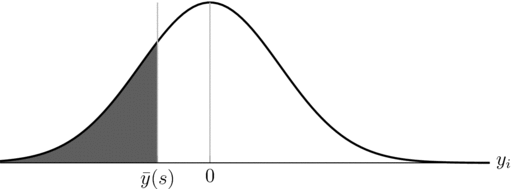
FIGURE 2. Political Action when Leader is Bad
If instead, the leader is actually the good type (θ = 1) then the mean of this distribution is given by g > 0. The distribution is shifted to the right, and the fraction of the population that is mobilized to protest is smaller. In Figure 3 we see that the fraction of the population that mobilizes when in fact θ = 1 is given by the dark region, or more precisely,
![]() $\Phi (\scriptsize\frac{\bar{y}^*(s)-g}{\sigma _y} )$
.
$\Phi (\scriptsize\frac{\bar{y}^*(s)-g}{\sigma _y} )$
.

FIGURE 3. Political Action for Both Types of Leader
If the number protesting when the leader is bad (the light region) is larger than T, the threshold for leader removal, but the number protesting when the leader is good (the dark region) is smaller than T, then under the equilibrium strategies of the citizens, good types are retained and bad types are removed. More precisely, leaders of type θ = 1 are retained, and leaders of type θ = 0 are removed in equilibrium if
![]() $\Phi (\frac{\bar{y}^*(s)-g}{\sigma _y} ) \le T \le \Phi (\frac{\bar{y}^*(s)}{\sigma _y} )$
.
$\Phi (\frac{\bar{y}^*(s)-g}{\sigma _y} ) \le T \le \Phi (\frac{\bar{y}^*(s)}{\sigma _y} )$
.
To ensure that each citizen is playing a best response, we need only check that the threshold is chosen to make recipient of that signal indifferent between mobilization and not. Then ai = 1 if and only if
 $$\begin{eqnarray*}
&&Pr(\theta =1|y_{i,1},s)g + Pr(\theta =0|y_{i,1},s)[pg + \beta ]\\
&&\quad - \kappa \ge Pr(\theta =1|y_{i,1},s)g + Pr(\theta =0|y_{i,1},s)pg \\
\end{eqnarray*}$$
$$\begin{eqnarray*}
&&Pr(\theta =1|y_{i,1},s)g + Pr(\theta =0|y_{i,1},s)[pg + \beta ]\\
&&\quad - \kappa \ge Pr(\theta =1|y_{i,1},s)g + Pr(\theta =0|y_{i,1},s)pg \\
\end{eqnarray*}$$
Consider first the left-hand side of this inequality, the expected utility from engaging in protest: If the leader is good, θ = 1, then she will be retained and in the second period she will choose G 2 = g—hence the first term on the left-hand side. In the instance that the leader is a bad type, θ = 0, the leader is removed in equilibrium. With probability p, a good type enters, and chooses G 2 = g; otherwise G 2 = 0. In addition, there is the benefit of joining a successful insurrection, of an amount β, but protest costs κ in any case.
We now turn our attention to the right-hand side, the expected utility from staying off the streets: Recall that there is a continuum of citizens and hence no citizen is pivotal. Good leaders are still retained, and poor ones are removed. If the leader is good, the citizen will still receive g if she does not protest; if the leader is bad, the leader is still removed, and (nonprotesting) citizen receives g if the leader is replaced with a new good leader, which occurs with probability p. Setting these two conditions equal to each other yields the private signal that leaves the citizen indifferent between protesting and not:
The citizen receiving private signal
![]() $\bar{y}^*(s)$
is indifferent between protesting and not. Therefore, any citizen receiving a private signal
$\bar{y}^*(s)$
is indifferent between protesting and not. Therefore, any citizen receiving a private signal
![]() $y_{i,1} \le \bar{y}^*(s) = \bar{y}(s)$
protests (and doesn’t otherwise), and this is a best response to the behavior of the other citizens.
$y_{i,1} \le \bar{y}^*(s) = \bar{y}(s)$
protests (and doesn’t otherwise), and this is a best response to the behavior of the other citizens.
What if it is not the case that
![]() $\Phi (\scriptsize\frac{\bar{y}^*(s)}{\sigma _y}) \ge T > \Phi (\scriptsize\frac{\bar{y}^*(s)-g}{\sigma _y})$
? If
$\Phi (\scriptsize\frac{\bar{y}^*(s)}{\sigma _y}) \ge T > \Phi (\scriptsize\frac{\bar{y}^*(s)-g}{\sigma _y})$
? If
![]() $T \le \Phi (\scriptsize\frac{\bar{y}^*(s)-g}{\sigma _y})$
, the public signal s is sufficiently extreme (and low) to ensure that—even when the government is in fact a good (θ = 1) type—enough of the population will believe the reverse to ensure its removal. Since the distribution of ε
i
is common knowledge, all citizens will realize this, and will consequently always choose to mobilize, regardless of their private information. For each citizen, its better to join in an uprising that is guaranteed to be successful than not to do so.
$T \le \Phi (\scriptsize\frac{\bar{y}^*(s)-g}{\sigma _y})$
, the public signal s is sufficiently extreme (and low) to ensure that—even when the government is in fact a good (θ = 1) type—enough of the population will believe the reverse to ensure its removal. Since the distribution of ε
i
is common knowledge, all citizens will realize this, and will consequently always choose to mobilize, regardless of their private information. For each citizen, its better to join in an uprising that is guaranteed to be successful than not to do so.
Conversely, if
![]() $T > \Phi (\scriptsize\frac{\bar{y}^*(s)}{\sigma _y})$
, even when the government is in fact a bad type (θ = 0), an insufficient portion of the population will believe this to be the case to ensure its removal. The public signal s is sufficiently high that it will be impossible for a group of requisite size to coordinate an uprising. All citizens will realize this, and will never choose to mobilize, regardless of their private information. This leads to the definition of
$T > \Phi (\scriptsize\frac{\bar{y}^*(s)}{\sigma _y})$
, even when the government is in fact a bad type (θ = 0), an insufficient portion of the population will believe this to be the case to ensure its removal. The public signal s is sufficiently high that it will be impossible for a group of requisite size to coordinate an uprising. All citizens will realize this, and will never choose to mobilize, regardless of their private information. This leads to the definition of
![]() $\bar{y}(s)$
as in Definition 2 above, and the complete specification of the equilibrium in Proposition 1 above.
$\bar{y}(s)$
as in Definition 2 above, and the complete specification of the equilibrium in Proposition 1 above.
Comparative Statics: Enhancing Transparency
The crucial equilibrium threshold
![]() $\bar{y}(s)$
is a function of the public signal, s. Recall that we have an interior equilibrium (where some protest, and some do not) when
$\bar{y}(s)$
is a function of the public signal, s. Recall that we have an interior equilibrium (where some protest, and some do not) when
![]() $\Phi (\scriptsize\frac{\bar{y}^*(s)}{\sigma _y}) \ge T > \Phi (\scriptsize\frac{\bar{y}^*(s)-g}{\sigma _y})$
.
$\Phi (\scriptsize\frac{\bar{y}^*(s)}{\sigma _y}) \ge T > \Phi (\scriptsize\frac{\bar{y}^*(s)-g}{\sigma _y})$
.
Definition 3 Define
![]() $\underline{s}$
implicitly by
$\underline{s}$
implicitly by
![]() $T = \Phi (\frac{\bar{y}^*(\underline{s})-g}{\sigma _y} )$
and
$T = \Phi (\frac{\bar{y}^*(\underline{s})-g}{\sigma _y} )$
and
![]() $\bar{s}$
by
$\bar{s}$
by
![]() $T = \Phi (\frac{\bar{y}^*(\bar{s})}{\sigma _y} )$
.
$T = \Phi (\frac{\bar{y}^*(\bar{s})}{\sigma _y} )$
.
In the Online Appendix, we demonstrate that
![]() $\bar{s}$
and
$\bar{s}$
and
![]() $\underline{s}$
are well defined with
$\underline{s}$
are well defined with
![]() $\bar{y}(s) = -\infty$
if
$\bar{y}(s) = -\infty$
if
![]() $s \ge \bar{s}$
and
$s \ge \bar{s}$
and
![]() $\bar{y}(s)=\infty$
if
$\bar{y}(s)=\infty$
if
![]() $s \le \underline{s}$
.
$s \le \underline{s}$
.
For a sufficiently extreme and positive public signal of the government’s type (
![]() $s \ge \bar{s}$
), all citizens will disregard their private information and never mobilize. Conversely, for a sufficiently extreme and negative signal (
$s \ge \bar{s}$
), all citizens will disregard their private information and never mobilize. Conversely, for a sufficiently extreme and negative signal (
![]() $s \le \underline{s}$
), all citizens will always mobilize, even if some strongly believe the government to be a good type. For such extreme realizations, each citizen knows unrest will either be successful or not, and each citizen would rather jump on the bandwagon than hold firm to her beliefs. For a similar result, see Morris and Shin (Reference Morris and Shin2002).
$s \le \underline{s}$
), all citizens will always mobilize, even if some strongly believe the government to be a good type. For such extreme realizations, each citizen knows unrest will either be successful or not, and each citizen would rather jump on the bandwagon than hold firm to her beliefs. For a similar result, see Morris and Shin (Reference Morris and Shin2002).
In equilibrium, for any
![]() $s \ge \bar{s}$
, governments of all types are retained. For any
$s \ge \bar{s}$
, governments of all types are retained. For any
![]() $s \le \underline{s}$
, all governments are removed. For any
$s \le \underline{s}$
, all governments are removed. For any
![]() $s \in (\underline{s},\bar{s})$
, governments are removed if they are of type θ = 0 and retained if they are of type θ = 1.
$s \in (\underline{s},\bar{s})$
, governments are removed if they are of type θ = 0 and retained if they are of type θ = 1.
Thus, when θ = 0, the government will be removed if
![]() $s \le \bar{s}$
, which will occur with probability
$s \le \bar{s}$
, which will occur with probability
![]() $\Phi (\frac{\bar{s}}{\sigma _s})$
. When θ = 1, the government will only be removed if
$\Phi (\frac{\bar{s}}{\sigma _s})$
. When θ = 1, the government will only be removed if
![]() $s \le \underline{s}$
, which will occur with probability
$s \le \underline{s}$
, which will occur with probability
![]() $\Phi (\frac{\underline{s}-g}{\sigma _s})$
. We can therefore define the degree to which the public en masse effectively separates good from bad types as the discrimination
$\Phi (\frac{\underline{s}-g}{\sigma _s})$
. We can therefore define the degree to which the public en masse effectively separates good from bad types as the discrimination
![]() $=\Phi (\frac{\bar{s}}{\sigma _s}) - \Phi (\frac{\underline{s}-g}{\sigma _s})$
.
$=\Phi (\frac{\bar{s}}{\sigma _s}) - \Phi (\frac{\underline{s}-g}{\sigma _s})$
.
Proposition 2 Discrimination is strictly increasing in transparency (falling in σ s ).
As σ
s
falls (transparency rises),
![]() $\bar{y}^*$
shifts to the right while both the probability density functions depicted grow more tightly distributed around their respective means. The net effect of these two forces is such that the “improved” public signal increases the difference in the turnout for protest when leaders are bad relative to when they are good.
$\bar{y}^*$
shifts to the right while both the probability density functions depicted grow more tightly distributed around their respective means. The net effect of these two forces is such that the “improved” public signal increases the difference in the turnout for protest when leaders are bad relative to when they are good.
Bad leaders always attract higher levels of protest than good. We interpret this equilibrium effect as implying that autocratic leaders who experience poor economic outcomes are always more likely to be removed than those that experience good outcomes. Proposition 2 tells us that this difference should be rising in levels of transparency.
Corollary 1 In equilibrium, poor economic performance is associated with autocratic removal; and poor economic performance in more transparent environments leads to even higher likelihood of autocratic collapse in equilibrium.
We can also derive predictions about the unconditional relationship between transparency and leader survival. This unconditional probability can be expressed as
![]() $(1-p)\Phi (\frac{\bar{s}}{\sigma _s}) + p\Phi (\frac{\underline{s}-g}{\sigma _s})$
. With probability 1 − p, the government is of type θ = 0, and it will be removed with probability
$(1-p)\Phi (\frac{\bar{s}}{\sigma _s}) + p\Phi (\frac{\underline{s}-g}{\sigma _s})$
. With probability 1 − p, the government is of type θ = 0, and it will be removed with probability
![]() $\Phi (\frac{\bar{s}}{\sigma _s})$
. With probability p, the government is of type θ = 1, and it will be removed with probability
$\Phi (\frac{\bar{s}}{\sigma _s})$
. With probability p, the government is of type θ = 1, and it will be removed with probability
![]() $\Phi (\frac{\underline{s}-g}{\sigma _s})$
. For a range of parameter values, increasing values of transparency will increase this unconditional probability of successful mobilization:
$\Phi (\frac{\underline{s}-g}{\sigma _s})$
. For a range of parameter values, increasing values of transparency will increase this unconditional probability of successful mobilization:
Proposition 3 If
![]() $-\frac{\sigma _y}{g}ln(\frac{p\kappa }{(1-p)[\beta -\kappa ]}) < \Phi ^{-1}(T)$
, then there exists a level of
$-\frac{\sigma _y}{g}ln(\frac{p\kappa }{(1-p)[\beta -\kappa ]}) < \Phi ^{-1}(T)$
, then there exists a level of
![]() $\sigma _s \equiv \bar{\sigma _s}$
such that the unconditional probability of leader removal is increasing for low levels of transparency (
$\sigma _s \equiv \bar{\sigma _s}$
such that the unconditional probability of leader removal is increasing for low levels of transparency (
![]() $\sigma _s \ge \bar{\sigma _s}$
).
$\sigma _s \ge \bar{\sigma _s}$
).
Proposition 3 characterizes a sufficient, not a necessary, condition for transparency to have this effect. Transparency increases the risk of leader removal so long as mass mobilization is not too “easy.” Remark 1 serves to clarify this requirement:
Remark 1 As β → κ the probability of leader removal is rising in transparency for all
![]() $\sigma _s \in \mathbb {R}_+$
and for all T ∈ (0, 1).
$\sigma _s \in \mathbb {R}_+$
and for all T ∈ (0, 1).
As β → κ, citizens require a sufficiently poor signal of economic performance to ensure mobilization. If, on the other hand, β ≫ κ or T is low, then all citizens mobilize even when the public signal indicates that the economy is performing relatively well. Then the probability of a successful mass demonstration is very high. Our model doesn’t allow us to determine the effect of transparency on leader removal unambiguously in this case. Since incidences of successful mass protest are relatively rare, it seems safe to assume that—at least in the vast majority of cases—the conditions of Proposition 3 are satisfied, and transparency will empirically be associated with an increase in the unconditional probability of autocratic collapse.
Model Extension
In our baseline model, the leader’s type θ ∈ {0, 1} is wholly determinative of her strategy in equilibrium. In this model extension, we relax this assumption and consider circumstances under which bad types may have an incentive to pool with good—to set G 1 = 1 in order to increase their chances of surviving in office. The comparative statics documented in the baseline model survive in a separating equilibrium to this extension, in which a leader’s type determines his action. We characterize such an equilibrium below and document the conditions under which such an equilibrium exists.
Consider an interaction identical to that above, save only for the utility function of the leader L. Define L’s utility in each period t as
 $$\begin{eqnarray*}
u_{L,t}(G_t;\theta ) &=& \left\lbrace \begin{array}{l@{\hspace*{9pt}}l}1 + B&\text{if}\, G_t=\theta \, \text{and in office,}\\
B&\text{if}\, G_t\ne \theta \, \text{and in office,}\\
0&\text{otherwise,}\end{array}\right.\\
u_L&=& \sum _{t=1}^2 u_{L,t}(G_t;\theta ),
\end{eqnarray*}$$
$$\begin{eqnarray*}
u_{L,t}(G_t;\theta ) &=& \left\lbrace \begin{array}{l@{\hspace*{9pt}}l}1 + B&\text{if}\, G_t=\theta \, \text{and in office,}\\
B&\text{if}\, G_t\ne \theta \, \text{and in office,}\\
0&\text{otherwise,}\end{array}\right.\\
u_L&=& \sum _{t=1}^2 u_{L,t}(G_t;\theta ),
\end{eqnarray*}$$
where B > 0 denote the rents from office. L has a primitive preference for matching his action Gt with his type θ. L also prefers to retain office, and gain access to the rents B. Thus, L may deviate from his preferred choice of G 1 if doing so increases his chance of remaining in office.
We characterize a separating equilibrium to this game in the following proposition:
Proposition 4 If
![]() $\frac{1}{1+B} \ge \Phi (\frac{\bar{s}}{\sigma _s}) - \Phi (\frac{\underline{s}-g}{\sigma _s})$
then the following strategies and beliefs constitute a (separating) PBE to the extended model.
$\frac{1}{1+B} \ge \Phi (\frac{\bar{s}}{\sigma _s}) - \Phi (\frac{\underline{s}-g}{\sigma _s})$
then the following strategies and beliefs constitute a (separating) PBE to the extended model.
-
1. Gt = θ for t = 1, 2, and θ = 0, 1.
-
2. ai = 1 if
 $y_{i,1} \le \bar{y}(s)$
and ai
= 0 otherwise, for all i
$y_{i,1} \le \bar{y}(s)$
and ai
= 0 otherwise, for all i
-
3.
 $Pr(\theta =0|y_{i,1},s)=\frac{\phi (\frac{y_{i,1}}{\sigma _y})\phi (\frac{s}{\sigma _s})(1-p)}{p\phi (\frac{y_{i,1}-g}{\sigma _y})\phi (\frac{s-g}{\sigma _s}) + \phi (\frac{y_{i,1}}{\sigma _y})\phi (\frac{s}{\sigma _s})(1-p)}$
for all i (Bayes’ rule),
$Pr(\theta =0|y_{i,1},s)=\frac{\phi (\frac{y_{i,1}}{\sigma _y})\phi (\frac{s}{\sigma _s})(1-p)}{p\phi (\frac{y_{i,1}-g}{\sigma _y})\phi (\frac{s-g}{\sigma _s}) + \phi (\frac{y_{i,1}}{\sigma _y})\phi (\frac{s}{\sigma _s})(1-p)}$
for all i (Bayes’ rule),
where ϕ is the pdf of the standard normal and
![]() $\bar{y}(s)$
is defined in Definition 2.
$\bar{y}(s)$
is defined in Definition 2.
Strategies in the separating equilibrium to the extended model are exactly analogous to those described in the baseline model. Good leaders set Gt
= 1, as this both satisfies their primitive preference and maximizes their chance of retention. Bad types also play according to type, setting Gt
= 0. In the second period, this constitutes a dominant strategy. In the first, any gain in the chances of retention from providing the public good are more than offset by the losses of playing against type. Given that L plays according to type, each citizen i is faced with exactly the informational difficulties described above. Each i thus chooses to turn to the streets if
![]() $y_{i,1}<\bar{y}(s)$
and not to do so otherwise.
$y_{i,1}<\bar{y}(s)$
and not to do so otherwise.
However, a separating equilibrium to the extended model only exists for a subset of parameter values. More precisely, a separating equilibrium exists only if the level of transparency is sufficiently low (σ
s
is sufficiently high) relative to the value of holding office B. We define the requisite value of σ
s
necessary for a separating equilibrium as
![]() $\tilde{\sigma }_s$
and characterize this value in the following proposition:
$\tilde{\sigma }_s$
and characterize this value in the following proposition:
Proposition 5 For any finite B ⩾ 0, there exists a
![]() $\tilde{\sigma _s}$
such that
$\tilde{\sigma _s}$
such that
![]() $\frac{1}{1+B} \ge \Phi (\frac{\bar{s}}{\sigma _s}) - \Phi (\frac{\underline{s}-g}{\sigma _s})$
for all
$\frac{1}{1+B} \ge \Phi (\frac{\bar{s}}{\sigma _s}) - \Phi (\frac{\underline{s}-g}{\sigma _s})$
for all
![]() $\sigma _s \ge \tilde{\sigma _s}$
, where
$\sigma _s \ge \tilde{\sigma _s}$
, where
![]() $\bar{s}$
and
$\bar{s}$
and
![]() $\underline{s}$
are as defined in Definition 3.
$\underline{s}$
are as defined in Definition 3.
A separating equilibrium exists—and our findings hold—if values of
![]() $\sigma _s \ge \tilde{\sigma }_s$
(transparency is sufficiently low).
$\sigma _s \ge \tilde{\sigma }_s$
(transparency is sufficiently low).
Remark 2 For any finite B, a separating equilibrium exists for
![]() $\sigma _s \ge \bar{\sigma _s}$
, and in any separating equilibrium, all comparative statics characterized for the baseline model hold.
$\sigma _s \ge \bar{\sigma _s}$
, and in any separating equilibrium, all comparative statics characterized for the baseline model hold.
Our findings thus hold for a restricted range of the (B, σ s ) parameter space.
A range of pooling equilibria, in which bad types set G 1 = 1 in the hopes of securing retention, also exist for alternate parameter values in the extended model. We characterize such equilibria in the Online Appendix. Our comparative statics do not hold in the pooling equilibrium.
Empirically, autocratic governments tend to be opaque (Hollyer, Rosendorff, and Vreeland Reference Hollyer, Rosendorff and Vreeland2011). However, we empirically examine the possibility that levels of transparency may rise to such levels that a separating equilibrium no longer exists by allowing for a nonmonotonic relationship between levels of transparency and the hazard of regime collapse due to unrest or democratization. We find no evidence for a nonmonotonic relationship. The hazard of regime collapse is monotonically increasing in transparency. We present these results in the Online Appendix.
EMPIRICS
Data Description
Our theoretical model depicts authoritarian collapse as the removal of the authoritarian regime or ruling clique. Empirically, we define such instances of collapse using Svolik’s (Reference Svolik2012) dataset on the duration of authoritarian regimes. Following Svolik, we define an instance of authoritarian collapse as the removal of an autocratic leader by an alternative leader or coalition not politically affiliated with the sitting clique. Since our theoretical mechanism operates via mass unrest, we focus particularly on instances of leader removal brought about by mass revolt or that lead to democratization.
Many works treat democratization as the result of the manifestation or threat of popular unrest (for instance, Acemoglu and Robinson Reference Acemoglu and Robinson2006; Boix Reference Boix2003; Przeworski Reference Przeworski2009; Rosendorff Reference Rosendorff2001). Others (e.g., Ansell and Samuels Reference Ansell and Samuels2010; Lizzeri and Persico Reference Lizzeri and Persico2004; Llavador and Oxoby Reference Llavador and Oxoby2005) contest this claim. Adjudicating this dispute is well beyond the scope of this article. We group these two forms of removal—mass revolt and democratization—together because separate analyses run on each produce similar results. More precisely, transparency is significantly associated with autocrat removal via revolt only (see Table 5 in the Online Appendix), and is positively associated with democratization as defined by Svolik, though these results do not obtain conventional levels of statistical significance (see Table 6 in the Online Appendix). According to an alternative definition of democracy developed by Cheibub, Gandhi, and Vreeland (Reference Cheibub, Gandhi and Vreeland2010), transparency is significantly associated with democratization (see Table 2). The definition of democracy employed by Cheibub et al. records more transitions during our time frame than does Svolik, thus the greater robustness of our results using the latter measure is likely explained by the increased degrees of freedom.
Our empirical specifications are designed to attempt to control for alternative mechanisms that may drive the relationship between transparency and regime collapse—particularly to adjust for the danger that liberalizing autocracies may be particularly prone to collapse. The danger of reverse causality—that some states choose to liberalize (disclose more information) in response to popular discontent—is particularly acute. This danger is somewhat mitigated by the nature of our measure of transparency, which varies far more across autocratic regimes than over time. (The average longitudinal standard deviation in transparency across countries is 25% of the overall standard deviation.) Moreover, any such reverse causality would tend to bias against our findings. If autocratic leaders disclose more information in response to public pressure, one would expect that transparency would have the effect of dissipating unrest. To the extent that such efforts are undertaken, our results at least indicate that they are unsuccessful. We additionally include a variety of controls in our empirical specifications to adjust for other forms of liberalization which might be undertaken in response to public pressure.
Hollyer, Rosendorff, and Vreeland (Reference Hollyer, Rosendorff and Vreeland2015b) demonstrate that variation in HRV index scores are driven primarily by characteristics of the regime. It does not appear to be the case that disclosures are systematically higher in good economic times. They find that growth is not a significant predictor of longitudinal variation in HRV scores.Footnote 19 Indeed, Hollyer, Rosendorff, and Vreeland (Reference Hollyer, Rosendorff and Vreeland2015b) find that, of a variety of economic and political controls that vary longitudinally, only a measure of whether a new leader has been seated in office is a significant predictor of disclosure under autocratic rule.
We draw several control variables pertaining to autocratic political institutions from the Democracy and Development (DD) dataset (Cheibub, Gandhi, and Vreeland Reference Cheibub, Gandhi and Vreeland2010). In all specifications, we control for an indicator variable
![]() $\text{Party} \in \lbrace 0,1\rbrace$
equal to 1 if multiple parties hold positions in the legislature.Footnote
20
We include this control given evidence that autocratic regimes that consist of multiple parties face substantially different risks, and exhibit different behaviors, than those that do not (Gandhi Reference Gandhi2008; Gandhi and Przeworski Reference Gandhi and Przeworski2006, Reference Gandhi and Przeworski2007; Svolik Reference Svolik2012). We also draw upon an indicator
$\text{Party} \in \lbrace 0,1\rbrace$
equal to 1 if multiple parties hold positions in the legislature.Footnote
20
We include this control given evidence that autocratic regimes that consist of multiple parties face substantially different risks, and exhibit different behaviors, than those that do not (Gandhi Reference Gandhi2008; Gandhi and Przeworski Reference Gandhi and Przeworski2006, Reference Gandhi and Przeworski2007; Svolik Reference Svolik2012). We also draw upon an indicator
![]() $\text{Military} \in \lbrace 0,1\rbrace$
, equal to 1 if the head of government is a representative of the military, given that autocracies headed by the military exhibit differential behaviors from those controlled by civilians (Davenport Reference Davenport2007; Svolik Reference Svolik2012; Wright Reference Wright2008).Footnote
21
$\text{Military} \in \lbrace 0,1\rbrace$
, equal to 1 if the head of government is a representative of the military, given that autocracies headed by the military exhibit differential behaviors from those controlled by civilians (Davenport Reference Davenport2007; Svolik Reference Svolik2012; Wright Reference Wright2008).Footnote
21
In all specifications involving incidents of mass mobilization and unrest, we draw our outcome variables from the Cross National Time Series Archive (Banks Reference Banks1979), as made available by Bueno de Mesquita et al. (Reference Bueno de Mesquita, Smith, Siverson and Morrow2003). These data consist of counts of the number of antigovernment demonstrations, strikes, riots, guerrilla movements, revolutions, assassinations, and coups in a given country in a given year. The Banks dataset derives these counts from archives of the New York Times. We consider antigovernment demonstrations and strikes to be clear manifestations of mass mobilization directed at the government. And we consider coups and assassinations to be clear examples of instability not requiring popular mobilization.Footnote 22
We additionally control for a variety of economic factors. Importantly, we control for GDP per capita, measured in thousands of purchasing power parity 2005 US dollars. This measure is included given the significant debate over modernization theory—the role of economic development in facilitating democratization (see, for instance Acemoglu et al. Reference Acemoglu, Johnson, Robinson and Yared2009; Ansell and Samuels Reference Ansell and Samuels2010; Boix Reference Boix2003; Przeworski and Limongi Reference Przeworski and Limongi1997; Przeworski et al. Reference Przeworski, Alvarez, Cheibub and Limongi2000). We also include this term due to the possibility that states’ capacity to collect and disseminate data may increase with economic development, so per capita income may act as a confound in our specifications. We additionally include measures of economic growth (the percentage change in real GDP per capita) in all models as a measure of government’s economic performance. Finally, we include a measure of economic openness (
![]() $\frac{\text{Exports}+\text{Imports}}{\text{GDP}}$
). This control is valuable given potential linkages between economic and political liberalization, and given that open economies are more likely to be subject to exogenous shocks to economic performance than closed, and thus economic performance may be less valuable a signal of government competence as trade dependence rises (Duch and Stevenson Reference Duch and Stevenson2008).
$\frac{\text{Exports}+\text{Imports}}{\text{GDP}}$
). This control is valuable given potential linkages between economic and political liberalization, and given that open economies are more likely to be subject to exogenous shocks to economic performance than closed, and thus economic performance may be less valuable a signal of government competence as trade dependence rises (Duch and Stevenson Reference Duch and Stevenson2008).
These economic measures are all drawn from the Penn World Table (PWT) version 6.3 (Heston, Summers, and Aten Reference Heston, Summers and Aten2009). The PWT offers several advantages as a measure of economic performance for this study: First, the PWT data are adjusted and interpolated by external researchers with no affiliation to reporting governments (though, the underlying data are still based on national accounts).Footnote 23 The PWT can thus be seen as a proxy for true economic performance (Gt or—equivalently—the incumbent’s type θ in our model) rather than as a realization of the public signal s.
Second, country time series included in the PWT are uninterrupted. This is important when employing a measure of data missingness as an explanatory variable. Were missing data present in the PWT, it is likely that missing values would correlate with transparency levels. Listwise deletion would therefore censor variation in a key explanatory variable, potentially inflating standard errors and understating measures of model fit.
Finally, we include a control for fuel exports, drawn from Easterly and Sewadeh (Reference Easterly and Sewadeh2001). This control is included given the resource curse hypothesis, which finds that fuel exports are negatively correlated with democracy and promote autocratic longevity (Jensen and Wantchekon Reference Jensen and Wantchekon2004; Ross Reference Ross1999).
Transparency, Mass Unrest and Autocratic Instability
In this section of the article, we test our claims that (1) transparency is associated with an increased probability of the collapse of autocratic leaders and (2) that transparency enhances the association between economic performance and regime instability. Economic growth maps into the parameter Gt (or, equivalently, the leader’s type θ) in our model. In equilibrium, leaders who perform more poorly in office are more likely to removed—poor growth should predict regime collapse. Proposition 2 establishes that this relationship between growth and collapse should grow stronger as transparency rises. And Proposition 3 establishes that transparency should have a direct effect on increasing the risk of regime removal.
Our empirical interest is in the danger that mass mobilization poses to ruling cliques. Our model does not speak to the threat leaders face from coups or military interventions, nor does it speak to the risks of intervention by foreign powers or resulting from civil wars. Our analysis therefore relies on a Cox competing hazards model of regime removal.Footnote 24 Our model estimates the probability that the ruling clique is unseated by a revolt or transitions to democracy in year t conditional on not already having done so. Alternative mechanisms of regime collapse act as competing risks. We estimate our model on all autocratic regimes in Svolik’s (Reference Svolik2012) dataset, but those regimes that exit via other methods are treated as censored after their death.Footnote 25 The unit of observation is the autocratic regime-year, where autocratic regimes are defined in accordance with Svolik (Reference Svolik2012).
We fit a model of the form
 $$\begin{eqnarray}
h_i(t) &=& h_0(t)\text{exp}(\gamma \text{Transparency}_{l,t-1} + \delta \text{Growth}_{l,t-1}\nonumber\\
&& +\, \mu \text{Transparency}_{l,t-1} \times \text{Growth}_{l,t-1} \nonumber \\
&&+\, \mathbf {X_{l,t-1} \beta }),
\end{eqnarray}$$
$$\begin{eqnarray}
h_i(t) &=& h_0(t)\text{exp}(\gamma \text{Transparency}_{l,t-1} + \delta \text{Growth}_{l,t-1}\nonumber\\
&& +\, \mu \text{Transparency}_{l,t-1} \times \text{Growth}_{l,t-1} \nonumber \\
&&+\, \mathbf {X_{l,t-1} \beta }),
\end{eqnarray}$$
where l denotes autocratic regime, t denotes time, h 0(t) is the baseline hazard function, and Xl, tβ is the product of a data vector and a corresponding vector of coefficients.Footnote 26 Time, in this instance, is defined as the number of years the autocratic regime has served in office. All errors are clustered by autocratic regime.
Our analysis is complicated by the presence of autocratic regimes that have experienced prior instances of instability in the data. Past instability may influence current stability. Our preferred approach to dealing with this issue is to employ conditional gap time models, in which the baseline hazard is estimated separately for autocratic regimes in states that experienced prior autocratic collapses and in states that have not (Box-Steffensmeier and Zorn Reference Box-Steffensmeier and Zorn2002). In so doing, we allow both the level and the shape of the baseline hazard to vary depending on past experiences of instability.Footnote 27 In one set of models, we separately estimate the baseline hazard conditional on whether there has been a prior autocratic collapse; in another, we estimate separate baseline hazards based on the number of instances of collapse;Footnote 28 and in a final specification we simply control for whether there has been a prior collapse.
Results from the model described by Equation (3) are presented in Table 1. The table reports coefficient values—not hazard ratios—so a positive coefficient indicates that a given covariate increases the risk of autocratic collapse (via revolt or democratization), while a negative coefficient indicates the reverse. In all models, we include controls for higher order polynomials of economic openness (
![]() $\frac{\text{Ec}. \text{Openness}^2}{100},\, \frac{\text{Ec}. \text{Openness}^3}{10,000}$
) to adjust for violations of the proportional hazards assumption, in keeping with the recommendations of Keele (Reference Keele2010). The coefficient on transparency is significant at the 10 percent level or higher in all models, except when we include all control variables. These controls are not themselves statistically significant, and the coefficient on transparency is stable across all specifications. We therefore expect that their inclusion leads to inefficiency, while their exclusion does not appear to cause bias.
$\frac{\text{Ec}. \text{Openness}^2}{100},\, \frac{\text{Ec}. \text{Openness}^3}{10,000}$
) to adjust for violations of the proportional hazards assumption, in keeping with the recommendations of Keele (Reference Keele2010). The coefficient on transparency is significant at the 10 percent level or higher in all models, except when we include all control variables. These controls are not themselves statistically significant, and the coefficient on transparency is stable across all specifications. We therefore expect that their inclusion leads to inefficiency, while their exclusion does not appear to cause bias.
TABLE 1. Cox Models, Autocrat Removal from Below

Notes: Cox competing hazards regressions of the hazard of autocratic removal via revolt or democratization. The models depicted in the first three columns, the middle three columns, and the last three columns differ in the manner in which they deal with countries that experienced multiple autocratic failures. Those in the first three columns report a conditional gap time model wherein the baseline hazard is separately estimated for regimes that experience a prior regime failure and for those that did not. Those in the next two columns estimate separate baseline hazards based on a categorical measure that reflects the number of prior collapses. Those in the final three columns simply control for prior collapses, rather than stratifying the baseline hazard. In all models, * denotes significance at the 10 percent level, ** denotes significance at the 5 percent level, and *** denotes significance at the 1 percent level. 95 percent confidence intervals are presented in brackets. All standard errors have been clustered by autocratic regime.
The estimated coefficient on Transparency is large and positive in all models. All estimates place the bulk of the posterior probability mass above zero —p values range from a high of 0.17 to a low of 0.05 across all specifications. The models with higher p values include several insignificant controls that reduce efficiency. Our point estimates suggest that a one standard deviation increase in the level of Transparency increases the hazard of autocratic collapse by between 40 and 50 percent.
The coefficient on economic growth is negative and significant in all but one model. In keeping with theoretical expectations, autocratic governments that inspire economic growth are at lower risk of collapse than those that do not achieve economic success. A one standard deviation increase in the growth rate is associated with a reduction in the risk of revolt of between 30 and 50 percent.
Our theoretical expectations further contend that the relationship between growth and the hazard of regime collapse should be conditional on the level of transparency. We thus include interactions of growth and transparency in all models. This estimate is negative in all nine models estimated, and is substantively meaningful. Moreover, the functional form of the Cox model implies an interactive effect of transparency and growth. Even without the interactive term, the functional form of our model assumes that the relationship between growth and regime removal is conditional on transparency in the manner expected theoretically (for a discussion, see Ai and Norton Reference Ai and Norton2003; Berry, DeMeritt, and Esarey Reference Berry, DeMeritt and Esarey2010; Greene Reference Greene2010; Nagler Reference Nagler1991).
To better grasp the relationship between transparency, growth, and autocratic collapse, we plot smoothed estimates of the hazard function—based on Model 8—for different values of growth and transparency in Figure 4, holding all other variables at their means (with the exception of Party and Military, which are held at 0, and Ever Collapse, which is held at 1). We also run Monte Carlo simulations based on this model. The results point to a substantively meaningful conditioning role for transparency on the relationship between growth and regime collapse. A shift from the 10th to the 90th percentile of growth shifts the multiplier for the baseline hazard by − 0.64 (s.d., 0.42) when transparency is 10th percentile. By contrast, when transparency is at its 90th percentile, the analogous shift in growth reduces the multiplier on the baseline hazard by − 2.13 (s.d., 3.36). These differences, however, are not precisely estimated—they are suggestive, but do not attain conventional standards of significance.

FIGURE 4. Hazard Rates as a Function of Transparency and Growth
We additionally explore the relationship between transparency and an alternative form of autocratic stability: the duration of continued autocratic rule. Autocratic collapse, in this instance, is defined as democratization. Time is defined as the number of years of continuous autocratic rule. We define both concepts using the DD dataset (Cheibub, Gandhi, and Vreeland Reference Cheibub, Gandhi and Vreeland2010).
As with our baseline results, we fit conditional gap time models to these data. We stratify the hazard based on a past history of instability—here defined by the presence/absence or frequency of past transitions to democracy. We additionally fit a Cox model only to regimes that have never previously experienced democracy. Results are presented in Table 2.
TABLE 2. Cox Model of Democratic Transitions, DD Definitions

Notes: Cox proportional hazards regressions of the hazard of transition to democracy, where democracy and autocracy are defined by the Democracy and Development dataset (Cheibub, Gandhi, and Vreeland Reference Cheibub, Gandhi and Vreeland2010). Models in the first two columns report a conditional gap time model wherein the baseline hazard is separately estimated for regimes that experience a prior regime failure and for those that did not. Those in the next two columns estimate separate baseline hazards based on a categorical measure that reflects the number of prior collapses. Those in the final two columns simply control for prior collapses. In all models, * denotes significance at the 10 percent level, ** denotes significance at the 5 percent level, and *** denotes significance at the 1 percent level. 95 percent confidence intervals are presented in brackets. All standard errors have been clustered by autocratic spell.
Results using this definition of transition are substantively similar to those in our baseline specifications. Transparency has a robust direct effect—it increases the hazard of democratization. It has a substantively large, but insignificant, conditioning role on the relationship between growth and democratization—growth is more important to survival when transparency is high. And growth significantly reduces the hazard of transition. These results are somewhat more precisely estimated than our baseline specification, likely because the DD dataset codes more transitions than Svolik codes regime failures. Consequently, we have more degrees of freedom with which to fit this model.
In the Online Appendix, we present analogous models of the relationship between transparency, economic growth, and other forms of regime collapse. The results from these models indicate that while our findings hold with respect to autocratic collapse as brought about via mass mobilization or democratization, they do not hold for other forms of regime instability. Indeed, transparency appears to be negatively associated with the risk of a coup. It is not the case that those autocratic regimes who disclose data are systematically “weak”—it appears that transparency is specifically associated with threats to the regime originating from the mobilization of the populace.
Robustness Checks
In the Online Appendix, we additionally present a variety of alternative specifications of our baseline model as robustness checks. We particularly seek to rule out the possibility that transparency is a product of broader attempts at autocratic liberalization, and that such liberalization itself is associated with regime stability.
In our baseline specifications, we control for economic liberalism using
![]() $\frac{\text{Exports}+\text{Imports}}{\text{GDP}}$
. However, this term is influenced by factors other than government policy—for instance, country size and access to the sea. One may be concerned that some autocratic regimes rely, in part, on economic performance to legitimate the regime, and these regimes pursue systematically more liberal economic policies. If, as is likely, these regimes are systematically more transparent, growth may play an enhanced role in regime survival in these cases as economic performance is the basis of popular support. In our robustness checks, we substitute for the
$\frac{\text{Exports}+\text{Imports}}{\text{GDP}}$
. However, this term is influenced by factors other than government policy—for instance, country size and access to the sea. One may be concerned that some autocratic regimes rely, in part, on economic performance to legitimate the regime, and these regimes pursue systematically more liberal economic policies. If, as is likely, these regimes are systematically more transparent, growth may play an enhanced role in regime survival in these cases as economic performance is the basis of popular support. In our robustness checks, we substitute for the
![]() $\frac{\text{Exports}+\text{Imports}}{\text{GDP}}$
measure using the economic restrictions component of the KOF Index of Globalization (Dreher Reference Dreher2006), and using an updated variant of the Sachs-Warner measure of economic openness (Sachs and Warner Reference Sachs and Warner1995) composed by Wacziarg and Welch (Reference Wacziarg and Welch2008).
$\frac{\text{Exports}+\text{Imports}}{\text{GDP}}$
measure using the economic restrictions component of the KOF Index of Globalization (Dreher Reference Dreher2006), and using an updated variant of the Sachs-Warner measure of economic openness (Sachs and Warner Reference Sachs and Warner1995) composed by Wacziarg and Welch (Reference Wacziarg and Welch2008).
Across all specifications, the point estimates on the transparency, growth, and interaction terms are largely unchanged relative to the baseline. Moreover, the coefficients on the control terms added as robustness checks are not themselves significant. In some instances, the standard errors on the transparency term are slightly inflated due to the presence of controls; p values on the transparency term range from 0.08 to 0.18. The robustness checks produce no evidence of bias in the baseline model: point estimates on the effect of transparency are unchanged and the controls are not themselves significantly associated with transparency, though some robustness checks are less efficient than the baseline model.
Transparency and Unrest
We have established that more transparent autocracies are more likely to experience regime failures than less transparent autocracies. We have suggestive evidence that the magnitude of the relationship between growth on the hazard of regime collapse is greater under more transparent regimes. These findings are consistent with theoretical predictions, but they constitute only indirect evidence that transparency can lead to mass unrest under autocracy.
To more directly test the model’s mechanisms, we examine the relationship between transparency and the frequency of various forms of domestic unrest under autocratic rule: namely, general strikes and antigovernment demonstrations.
We also examine the relationship between transparency and forms of unrest not involving mass mobilization, such as assassinations, coups, guerrilla warfare, and revolutions, which tend to be executed by a small elite or counterelite.Footnote 29 Our model offers no predictions regarding the relationship between transparency and these alternative forms of unrest. Nonetheless, confidence that our results are driven by the posited mechanism should be reinforced if we do not find a systematic relationship between transparency and forms of unrest that do not involve mass mobilization.
It is particularly important to examine these relationships given the danger of a form of selection bias in our results. One could imagine a competing theoretical account, which holds that citizens demand transparency from autocratic governments. When these governments are relatively weak, leaders may capitulate to these demands in exchange for greater citizen support. If these relatively weak autocrats are also more prone to collapse, one might imagine that our results from the previous section were driven by omitted variable bias.
Our results in this section speak to this concern in two ways. First, if weak governments capitulate to citizen demands by granting transparency, the relationship between mass mobilization and transparency will tend to be biased toward zero. Governments only increase levels of transparency to drive down the risk of citizen unrest and would presumably cease such reform efforts if these prove systematically ineffective. So, if we find a positive relationship between transparency and mass unrest, one must conclude that any such bias must be relatively small. Second, weak autocrats are likely to be prone to a variety of forms of instability, not just to protests and strikes. If we do not observe a relationship between transparency and these other forms of unrest, we can say with increased confidence that the relationship between transparency and democratization is mediated by mobilization.
To test the relationship between transparency, growth, and the incidence of unrest, we rely on country fixed-effects negative binomial regressions of the Banks (Reference Banks1979) measures of unrest on the previously described measures of transparency, growth, and their interaction, as well as a host of controls. We employ a negative binomial because the Banks data are measured as count variables, and because the data are likely to be overdispersed due to the large number of zero-valued observations.Footnote 30
Our empirical model is thus
 $$\begin{eqnarray}
\text{Unrest}_{c,t} &=& \text{FENegBin}(\rho \text{Unrest}_{c,t-1} \nonumber \\
&&+\, \eta \text{Transparency}_{c,t-1} + \zeta \text{Growth}_{c,t-1} \nonumber \\
&&+\, \xi \text{Transparency}_{c,t-1} \times \text{Growth}_{c,t-1} \nonumber \\
&&+\, \mathbf {X_{c,t-1}\nu }+ \mathbf {T\iota })
\end{eqnarray}$$
$$\begin{eqnarray}
\text{Unrest}_{c,t} &=& \text{FENegBin}(\rho \text{Unrest}_{c,t-1} \nonumber \\
&&+\, \eta \text{Transparency}_{c,t-1} + \zeta \text{Growth}_{c,t-1} \nonumber \\
&&+\, \xi \text{Transparency}_{c,t-1} \times \text{Growth}_{c,t-1} \nonumber \\
&&+\, \mathbf {X_{c,t-1}\nu }+ \mathbf {T\iota })
\end{eqnarray}$$
where c denotes country, t year, T a cubic polynomial of time, ι is a vector of associated coefficients, Xc, t − 1 is a vector of controls, and ν is a vector of associated coefficients. We include a cubic polynomial of time to control for the potential confounding effects of time trends using a general functional form. And we include a lagged dependent variable in all specifications to adjust for the dynamics of the data generating process (Beck and Katz Reference Beck and Katz2011).
Results from the model specified in Equation (4) are reported in Table 3. To ensure our results are robust to possible overfitting, we also present models dropping controls in Table 4.
TABLE 3. Fixed-Effects Negative Binomial Models, Unrest

Notes: Fixed-effects negative binomial regressions of levels of unrest as a function of transparency and growth. Measures of unrest are drawn from Banks (Reference Banks1979). All models include a lagged dependent variable, the coefficient on which is reported in the first row of the table. *Significance at the 10 percent level. **Significance at the 5 percent level. ***Significance at the 1 percent level. 95 percent confidence intervals are presented in brackets.
TABLE 4. Fixed-Effects Negative Binomial Models, Unrest

Notes: Fixed-effects negative binomial regressions of levels of unrest as a function of transparency and growth. Measures of unrest are drawn from Banks (Reference Banks1979). All models include a lagged dependent variable, the coefficient on which is reported in the first row of the table. *Significance at the 10 percent level. **Significance at the 5 percent level. ***Significance at the 1 percent level. 95 percent confidence intervals are presented in brackets.
Increased levels of transparency are robustly associated with more frequent general strikes and demonstrations. It is also associated with more frequent riots, though, as we demonstrate below, this result is not robust to the inclusion of alternative controls. The direct association between transparency and the frequency of revolutions, guerrilla movements, coups, and assassinations is not significantly different from zero.
As noted above, the interpretation of transparency’s role in conditioning the effect of growth on unrest is not straightforward in nonlinear models. More precisely, when the estimated coefficient on the Transparency term is large and positive, the functional form of the model dictates that the marginal effect of a change in Growth will rise as values of Transparency increase. Monte Carlo simulations reveal that transparency plays an important conditioning role with respect to the association between growth rates and the frequency of general strikes. This conditioning effect is substantively large, though not significant. An increase in growth from its 10th to its 90th percentile is predicted to reduce the frequency of strikes by 0.06 (s.d. 0.08) when transparency is at its 10th percentile. When transparency is at its 90th percentile, by contrast, such a shift in growth is predicted to reduce the frequency of strikes by 1.4 (s.d. 1.5). Transparency plays an important direct role in the frequency of demonstrations, but does not display a substantively large or significant role in conditioning the relationship between growth and demonstrations. Similarly, transparency is directly related to the frequency of riots (though this result is not robust; see below), but does not play a conditioning role. And there is no conditioning or direct relationship between transparency and assassinations, guerrilla movements, or revolutions.
Robustness Checks
We present a variety of robustness checks for these results in the Online Appendix. These results face a particular risk, given our reliance on the Cross-National Time Series dataset (Banks Reference Banks1979) to code instances of unrest. These data are coded based on reporting in the New York Times and offer broad temporal and cross-country coverage. However, Schedler (Reference Schedler2012) documents that this methodology tends to undercount instances of unrest. A general tendency to undercount unrest would bias our results downward, but one may be concerned that the degree of measurement error is systematically correlated with our measure of transparency. If governments that disclose more information to the World Bank are also more open to Times reporters, perhaps instances of unrest are more severely undercounted in opaque countries than in transparent ones. If this is the case, our results would be biased upward as a result of measurement error.
The fact that we make predictions with regard to specific forms of unrest—antigovernment demonstrations and strikes—and not unrest in general, somewhat insulates our results from this concern. There is little reason to expect that such biases affect the reporting of demonstrations and strikes, but not coups or assassinations. However, we additionally run a series of robustness checks incorporating a control for freedom of the press. Specifically, we include a control for an indicator variable which takes the value of 1 if the press is coded as “Not Free” by Freedom House’s Freedom of the Press index.Footnote 31 The inclusion of this control somewhat truncates our time series—observations are only available from 1982.Footnote 32 We include an indicator for “Not Free” country years, rather than using the full range of the Freedom House index—“Free,” “Partially Free,” and “Not Free”—given that only 5% of country-year observations in our sample of autocracies are coded as Free. The central distinction in these data is between Partially Free and Not Free observations.
We report our findings using these measures in Tables 12 and 13 in the Online Appendix. In keeping with the dangers of biased reporting noted by Schedler (Reference Schedler2012), the coefficient on the Not Free indicator is consistently negative (excepting for counts of guerrilla movements) and is sometimes significant. Moreover, when we include the Not Free indicator in the regression exploring the frequency of riots, the indicator is significant while the coefficient on transparency declines in magnitude and is no longer significant. However, our finding that transparency is associated with an increased frequency of strikes and antigovernment demonstrations—but not with other forms of unrest—is unaffected by the inclusion of this control.
We additionally present robustness checks employing alternative measures of economic liberalization in the appendix in Tables 14– 17 in the Online Appendix. These alternative measures are identical to those described above in our robustness checks of our results on the stability of autocratic regimes. Our findings on strikes and antigovernment demonstrations are robust across all specifications.
CONCLUSION
Increased transparency—in the form of data dissemination—is associated with the instability of autocratic regimes. Transparent autocracies experiencing low levels of economic growth are particularly prone to collapse brought about either via mass revolt or transition to democracy. This association between transparency and regime instability appears to be driven by increased levels of mass mobilization. Transparency is associated with more frequent demonstrations and strikes under autocratic rule, but is not associated with more frequent coups, assassinations, or guerrilla movements.
These empirical findings are supportive of our theoretical account, which stresses the importance of data disclosure in coordinating citizen beliefs. Without such information, citizens are likely to be highly uncertain not only of the performance of their leaders, but also of other citizens’ willingness to mobilize. The information contained in publicly available aggregate economic data can serve to coordinate beliefs under autocratic rule.
These findings have implications for three literatures. First, they reinforce collective action-based accounts of mass mobilization—as opposed to those stressing the importance of structural factors or popular dissatisfaction with the incumbent government alone. Second, they have implications for a substantial literature on democratic transitions. Finally, we contribute to a growing literature on the role of transparency. We stress a novel mechanism by which transparency may affect political processes and government accountability.
When taken in combination with our results with regard to democracies in Hollyer, Rosendorff, and Vreeland (Reference Hollyer, Rosendorff and Vreeland2015a), our findings have an additional implication: The relationship between mass unrest and information is critically mediated by political institutions. Under democracy—an institutional arrangement that ensures citizens both have access to a mechanism other than unrest to discipline leaders and that citizens are well informed of the distribution of discontent—transparency serves to stabilize the regime. Transparency might be said to enhance democratic legitimacy—elections are better able to police agency problems in government when transparency is high, reducing citizen incentives to engage in unrest. By contrast, when alternative outlets for discontent are absent, and alternative sources of information are lacking, transparency serves to increase the frequency of unrest.
SUPPLEMENTARY MATERIAL
To view supplementary material for this article, please visit http://dx.doi.org/10.1017/S0003055415000428.











Comments
No Comments have been published for this article.